AST 1410 – Stars (2025)
Table of Contents
- 1. Syllabus
- 2. Master equations
- Thu 9 Jan (double lecture)
- What is a star?
- Implication: P high → T high → loose heat
- Basics of evolution: contraction, heat up, fusion
- Virial theorem: Eint=-½ Egrav; Etot=Eint+Egrav=½ Egrav
- Where do we see stars
- Structure equations: MC, HE, TE, EB
- Luminosity of a star
- Homology
- Real M-R and M-L relations
- Substantial difference: inert lump inside → shell source
- Timescales
- Mon Jan 13
- Thu 9 Jan (double lecture)
- 3. Equation of state
- 4. Heat loss
- 5. Energy production
- 6. Evolution of single stars
- Mon Feb 10 - Completely convective stars and the pre-main sequence
- Thu Feb 13 - evolution towards and on the main sequence
- Mon Feb 24 - Giant Branch and Helium Flash
- Thu Feb 27 - Intermediate Mass Giants, Blue Loops
- Mon Mar 3 - Asymptotic Giant Branch: Mcore-L relation and superwind
- Thu Mar 6 - Asymptotic Giant Branch: Shell flashes and Nucleosynthesis
- Mon Mar 10 and Thu Mar 13 - Overall Evolution, Supernovae
- 7. Binary evolution
1. Syllabus
- Lectures
- Mondays, 11-12; Thursdays, 11-13; AB113
- Lecturer
- Marten van Kerkwijk, MP 1203B, 416-946-7288, mhvk@astro (.utoronto.ca)
- Office hours
- By appointment, or just drop by my office
- Web page
-
http://www.astro.utoronto.ca/~mhvk/AST1410/ - notes
Stellar astrophyiscs – the success story of astronomy in the last century – requires a synthesis of most of basic physics (thermodynamics, quantum mechanics, and nuclear physics). It underlies nearly all of astronomy, from reionisation to galaxy evolution, from interstellar matter to planets, and from supernovae and planetary nebulae to white dwarfs, neutron stars, and black holes.
In this course, we will review these successes (roughly first eight weeks) and then discuss current topics and remaining puzzles (last four weeks, detailed content depending on interest).
Underlying Physics
- Master equations
- equilibria; timescales; mass-radius and mass-luminosity relations; Hertzbrung-Russell diagram, common threads in stellar evolution, features in stellar evolution.
- Equation of state
- fermions and bosons; pressure and energy density; ideal gas; (completely and partially) degenerate gas; radiation pressure; Boltzman distribution; Saha equation.
- Heat loss
- radiative diffusion; conduction; opacity sources; Schwarzschild and Ledoux criteria; mixing length theory; convective flux; stellar context for convection; semi-convection.
- Energy production
- nuclear binding energy; Coulomb barrier; reaction channels (PP, CNO, He and beyond, D/Li burning, s-/r-/p-processes); rates and neutrinos.
Stellar Evolution Themes
- Low-mass stars
- Hayashi track; Li burning; (former) solar neutrino problem; pressure ionization and thermal ionization; convection zone advance; rotational evolution; shell burning; core-mass radius, luminosity relations; helium core flash; thermal flashes; RGB/AGB winds; production of intermediate-mass elements; white dwarfs.
- High-mass stars
- CNO burning and core convection; Eddington luminosity and formation/mass loss of high mass stars; nucleosynthetic yield of high mass stars; rotational evolution; electron-capture, core collapse and pair instability SNe; Pop III stars; neutron stars, black holes.
- Binary evolution
- frequency of binarity; tidal synchronization and circularization; Roche lobe overflow; conservative and non-conservative mass transfer; common-envelope evolution; mergers; blue and red stragglers.
- Nucleosynthesis
- production of the elements; explosive nucleosynthesis; r and s process; core-collapse supernovae; thermonuclear supernovae; mergers; various dredge-ups; thermal pulses.
Course texts
The main book we will use is Stellar Structure and Evolution (KWW; Kippenhahn, Weigert & Weiss, Springer-Verlag, 2012; can download PDF, courtesy of UofT library). Especially for those who did not take undergraduate astrophysics, I strongly recommend An Introduction to Modern Astrophysics, by Carroll & Ostlie (2nd edition; Cambridge University Press, 2017). This book introduces more empirical knowledge (and jargon) assumed known in KWW, and is used for the UofT undergraduate courses AST 221 and AST 320. Below, I'll at times refer to relevant notes and mini problem sets from the latter.
Evaluation
- Two problem sets (30% total), due two weeks after posting.
The second will use
mesato investigate stellar evolution.- Problem set 1 (pdf), due Feb 27.
- Problem set 2 (pdf), due Mar 20.
- Short presentations (10% total) explaning a specific concept. (8 min., plus 7 min. discussion; see list of topics)
- Long presentation (20%) on a more advanced topic. Can be on any
topic (with approval), though here are some suggestions. Format
roughly that of TASTY (18 min + 7 min discussion).
- March 27: Grace, Joshua, Abigail, Nan
- April 3: Michael, Nolan, Mattias, Sarah
- Final exam (40%; oral).
2. Master equations
Equilibria; timescales; mass-radius and mass-luminosity relations; Hertzbrung-Russell diagram, common threads in stellar evolution, features in stellar evolution.
Thu 9 Jan (double lecture)
- Textbook
- Covered: KWW 1–2.4, 3.3, 4.4, 5.1.1, 5.1.2, 20 [AST 320 notes 1, 2].
- Read independently: KWW 2.5–2.6, 3.1.
- Exercises
- Check you understand the basics discussed so far.
- AST320 mini problem sets: I, VI
- E.g., check wiki:HRD, and think again why are there limits on the left (no regular stars hotter & dimmer than the main sequence), at the top (no ultra-luminous stars), and on the right (no very cool stars)?
- What mass-radius relation would you expect for a set of stars with the same central temperature? Would more massive stars have higher or lower central density and pressure?
- AST320 mini problem sets: III
- For fun, also have a look at AST320 mini problem set VII.
- Calculate dynamical time for the Sun (⟨ρ⟩≈1 g/cm3), a neutron star (∼1014 g/cm3), and the Universe as a whole (∼1 m-3≈10-30 g/cm3).
- Derive the Virial Theorem (assuming ideal gas) yourself, following hint below (before reading KWW 3.1).
- Check you understand the basics discussed so far.
- General knowledge questions
- (Questions we hope any astronomer can answer, from the former
general qualifier)
- Explain why we know what the Sun’s central temperature roughly ought to be, and how we know what it actually is.
- Which have higher central pressure, high-mass or low-mass main-sequence stars? Roughly, what is their mass-radius relation? Derive this.
- Why is nuclear fusion stable inside a main-sequence star?
- Derive the scaling of luminosity with mass for a (mostly) radiative star. Do you need to know the source of energy for the star to derive this scaling?
What is a star?
- Me: ball of gas
- wiki:Star: A star is a massive, luminous sphere of plasma held together by gravity.
Implication: P high → T high → loose heat
Unless high P without high T → degeneracy (brown dwarf, degenerate helium core, white dwarf).
Basics of evolution: contraction, heat up, fusion
When does it stop?
Virial theorem: Eint=-½ Egrav; Etot=Eint+Egrav=½ Egrav
- Roughly, one has Egrav ≈ GM2/R, Eint ≈ N⟨eint⟩ = (M/μmH)3/2 kT, hence kT ≈ GMμmH/R.
- To derive it formally, multiply HE by r on both sides and integrate over sphere; use that for ideal gas U = 3/2 nkT = 3/2 P.
Where do we see stars
Check wiki:HRD. Why are there limits?
- left: Tc very high → fusion (think of contraction gone too far)
- top: L too high, matter blown away (LEdd)
- right: T profile too steep → convection
Structure equations: MC, HE, TE, EB
- mass conservation: ∂m/∂r = 4πr2ρ
- Hydrostatic equilibrium: ∂P/∂r = -gρ = -Gmρ/r2
- Thermal equilibrium: ∂T/∂r = -(3/4ac)(κρ/T3)(ℓ/4πr2); easiest to derive from general diffusion equation: \(j = -\frac13 vl_{mfp} \nabla{}n\); for radiation, v=c, lmfp = 1/σn = 1/κρ, n = aT4; hence, Frad = ℓ/4πr2 = -c/3κρ ∂(aT4)/∂r, from which one can solve for ∂T/∂r.
- Energy balance: ∂ℓ/∂r = 4πr2ρε
- To solve, needs
- equation of state P(ρ,T,abundances)
- opacity κ(ρ,T,abundances)
- energy generation rate ε(ρ,T,abundances)
- If T (dependence) known, can solve MC, HE separately.
- Independent variable r or m (or P, or …)
Luminosity of a star
- Simple estimates/scalings:
- MC: ρ ≈ M/R3
- HE: P ≈ GM2/R4
- TE: L ≈ acRT4/κρ
- Combining with ideal gas law P=(ρ/μmH)kT:
- MC+HE: kT ≈ GMμmH/R
- MC+HE+TE: L ≈ acG4mH4 μ4M3/κ
Note: what is radiated does not depend on how energy is generated; star has to provide the energy, whether by contraction or fusion.
Homology
If two stars have the same structure, i.e., m'(r')/M'=m(r)/M for all r'/R' = r/R, then:
- MC: ρ'(r')/ρ(r) = (M'/M)(R'/R)-3
- HE: P'(r')/P(r) = (M'/M)2(R'/R)-4
One can also derive other properties; see KWW 20.
Real M-R and M-L relations
- ε steep function of T → M/R nearly constant. Reality R ∝ M0.8.
- κ not constant (higher at low T, but convection moderates the effect) → L ∝ M4
- contribution of degeneracy → steeper at low M
- contribution of radiation pressure → flatter at high M.
Substantial difference: inert lump inside → shell source
Or denser lump with fusion (say He core): ``star inside a star''
Timescales
- Dynamical: τdyn ≈ 1/(Gρ)1/2
What if not in HE?
Equation of motion: ρ∂v/∂t = ρ∂2r/∂t2 = -∇P + ρ∇Φ = -∂P/∂r -ρg
- Pressure drops away? τff ≈ (R/g)1/2 ≈ 1/(Gρ)1/2
- Gravity drops away? τexpl ≈ R(P/ρ)-1/2 ≈ R/cs ≈ 1/(Gρ)1/2
- Thermal: tth ≈ Eth/L (≈ GM2/RL for whole star)
If not in TE over some distance d: F = -(vlmfp/3)∇U ≈ (vlmfp/3)U/d (where vlmfp=c/κρ for diffusion by radiation).
Hence, timescale τadj ≈ Ud3/Fd2 ≈ 3Ud3/vlmfpUd ≈ d2/vlmfp ≈ (lmfp/v)(d/lmfp)2 (random walk: tstep Nsteps)
Timescale for radiative damping of pulsations? Higher order → smaller d → faster damping.
- Nuclear: tnuc ≈ Enuc/L
Mon Jan 13
Mostly discussed the general knowledge questions posed for last class.
- Textbook
- Covered: KWW 25.3 (esp. 25.3.2);
- Read independently: KWW 27 (formation of a protostar)
- Read ahead: KWW 19.1-19.4, 19.9, 15 (except 15.4).
- Exercises
- AST320 mini problem sets: II
- General knowledge questions
- Describe what happens as a cloud starts to collapse and form a star. What is the difference between the collapse and contraction stages? What happens to the internal temperature in both? When does the contraction phase end, and why does the end point depend on the mass of the object?
Stability
Upon compression, ρ∝R-3. Thus, for an adiabatic perturbation, P ∝ ργ ∝ R-3γ (with γ a suitable average over the star). To keep in HE, P should increase as R-4 or faster, i.e., 3γ>4 or γ>4/3.
3. Equation of state
Fermions and bosons; pressure and energy density; ideal gas; (completely and partially) degenerate gas; radiation pressure; Boltzman distribution; Saha equation.
Thu Jan 16
- Textbook
- KWW 19.1–19.4, 19.9 (and scan through rest except 19.11), 15 (except 15.4) [AST 320 notes 4, 3]
- Exercises
- Write your own polytrope integrator (you'll need it for the first problem set; I suggest using python; if you are clueless, have a look at my simple integrator for an isothermal atmosphere).
- Use it to calculate the radius of a star with a solar mass and with central density and pressure like the Sun, for n=1.5 and 3.
- AST320 mini problem sets: IV
- Further exercises
- For classical particles, show that n(p)dp is a Maxwellian, and that one recovers the ideal gas law.
- For photons, μ=0. Show that Uνdν equals the Planck functions, and that its integral equals aT4 (note: ∫0∞ dx x3/(exp(x)-1)=π4/15)
- General knowledge question
- What is a polytropic equation of state? Give examples of objects for which this is a very good approximation, and explain why it is.
Polytropes: P = Kργ ≡ Kρ1+1/n
For K, γ, n ≡ 1/(γ-1) constant, can integrate HE+MC.
Examples:
- Constant density (incompressible fluid)
- Isothermal (part)
- Completely convective
- Degenerate (K fixed)
For given K, n, know ρ(r), P(r), Eg, etc.; see AST 320 notes 4, esp. Table 4.1.
EOS: Pressure integral: P = (1/3) ∫p npvppdp
- NR: vpp→p2/m=2ep → P=(2/3)U → Virial Theorem: Eg=-2Ei, Etot=(1/2)Eg
- ER: vpp→cp=ep → P=(1/3)U → Virial Theorem: Eg=-Ei, Etot=0
- generally, np=n(ep)g(4πp2/h3)dp, n(ep)=1/[exp((e-μ)/kT) ± 1]
+1:Fermions; -1: bosons; μ: chemical potential; g: number of internal states (such as spin)
(For a nice description of the meaning of The elusive chemical potential μ, see Baierlein 2001AmJPh..69..423B.) - ignore ±1: classical particles → ideal gas law: P=(ρ/μmH)kT (μ here is mean molecular weight)
- photons: -1, μ=0 → get BB → P=(1/3)aT4
- electrons: +1: completely degenerate → fill up to pF = h(3n/4πg)1/3
- NRCD: P=K1(ρ/μemH)5/3, K1=(3/4πg)2/3(h2/5me)≈2.34×10-38 N m3
- ERCD: P=K2(ρ/μemH)4/3 K2=(3/4πg)1/3(hc/4)≈2.45×10-26 N m2
- Complications: molecular/atomic/nuclear dissociation, pair formation
- Combinations
- Simplest: whichever dominates, or at least add radiation
- Rough estimate everywhere (Paczynski 1983ApJ...267..315P:
- P = Pe+Pi+Prad = Pe+(ρ/μimH)kT +(1/3)aT4
- Pe = (P2e,ideal+P2e,cd)1/2, Pe,ideal=(ρ/μemH)kT
- Pe,cd = (P-2e,nrcd+P-2e,ercd)-1/2
- EOS from look-up table
- for completely ionised gas: Helmholtz (Timmes+Swesty 2000ApJS..126..501T; includes pair formation, explanation in Timmes+Arnett 1999ApJS..125..277T)
- MESA's eos module
Mon Jan 20
- Textbook
- Discussed in class: KW 14 (part of AST 320 notes 5)
- Read independently: KW 4.
- Exercises
- AST320 mini problem sets: V
Another way to think about ionisation, etc.
(Different from how I discussed it in class, which was based on KW 14.)
Consider a fixed volume V at a fixed temperature T (or, equivalently, constant ρ and T). In thermal equilibrium, systems go to their most probable state, i.e., one maximizes entropy, \(S=k \log Z\), where \(Z\) is the partition function, a sum over all possible states i, weighted by \(\exp(-E_i/kT)\). Usually, one can split contributions, e.g., for non-interacting photons, ions, and electrons, one has \(Z=Z_{\gamma}\times{}Z_{e}\times{}Z_{i}\) (and thus \(S=k\sum\log Z\)).
In the volume, for one particle at some momentum \(p\), the number of phase space elements available is \((V/h^3)\times4\pi{}p^{2}dp\), with a probability \(\exp(-\epsilon_p/kT)\). The total number of phase space elements is thus \(\sim{}(V/h^3)p_{th}^3\), where \(p_{th}\) is some typical momentum associated with the temperature. Doing the integral gives the Maxwellian and \(p_{th}=\sqrt{2\pi{}mkT}\). Maybe more insightful is follow Baierlein 2001AmJPh..69..423B and define a typical size, \(\lambda_{th}\equiv{}h/p_{th}\), the ``thermal De Broglie'' wavelength. Then, the number of possible states is simply \(V/\lambda_{th}^3\). For a set of N identical particles, the contribution to the partition function is thus \[Z_N=\frac{[g(V/\lambda_{th}^3)\exp(-\epsilon/kT)]^N}{N!},\] where \(g\) is the number of internal states, the factorial \(N!\) ensures we do not overcount states where two particles are swapped, and \(\epsilon\) is an energy cost beyond thermal kinetic energy there may be for having this particle.
Let's apply this to pair creation, assuming some mix of photons, ions, electrons and electron-positron pairs. Assuming a dilute plasma, their contributions to \(Z\) can be split, i.e., \(Z=Z_{\gamma}\times{}Z_{e}\times{}Z_{i}\times{}Z_{\pm}\) (of course, the physical picture is that there is a formation rate from the interactions of two photons, balanced by an annihilation rate; for the statistics, we are only concerned about the final equilibrium ). Since the electrons and positrons are independent, \(Z_{\pm}=Z_{+}\times{}Z_{-}\), with both given by the above equation with \(\epsilon=m_{e}c^2\), but with \(N_{+}=N_{-}=N_{\pm}\). Hence, \(Z_{+}=Z_{-}\), and to find the number of particles, we can just find the maximum of \(S_{+}=k\log{}Z_{+}\), i.e., \[\frac{\partial{}S_{+}}{\partial{}N_{+}} = \frac{\partial{}k\log Z_{+}}{\partial{}N_{+}} = \frac{\partial}{\partial{}N_{+}}kN_{+}\left[\log\left(g\frac{V}{\lambda_{th}^3}\right)-\frac{m_{e}c^2}{kT} -\log N_{+}-1\right]=0,\] where we used that for large \(N\), \(\log N!=N\log N - N\). Solving this for \(N_{+}\), one finds \[N=g\frac{V}{\lambda_{th}^3}\exp(-m_{e}c^2/kT).\] Equivalently, one has \(n\equiv{}N/V=g\exp(-m_{e}c^2/kT)/\lambda_{th}^3\), which has the nice implication that for classical particles, the probability for one with given internal state to exist in a given volume element \(\lambda_{th}^3\) is simple \(\exp(-\epsilon/kT)\). Thus, for this very small volume, the probability becomes significant for \(kT\approx{}m_{e}c^2\). But when does the number of pairs become significant on larger scales? One measure to use is when \(n_{\pm}=n_e\), i.e., when \(\exp(-m_{e}c^2/kT)=_{}\lambda_{th}^3 n_e/g\). For electrons (\(m=m_e\)), one has \(\lambda_{th}=2.4\times10^{-10}T_9^{-1/2}\) cm, and \(n_e=\rho/\mu_e{}m_H=6\times10^{23}(\rho_2/\mu_e)\) cm-3, so it requires \(T_{9}\approx{}m_{e}c^{2}/k(11.7+\log{}gT_9^{1/2}/\rho_2)\approx0.6\), quite consistent with KW, Fig. 34.1.
One can treat ionisation similarly, writing \(Z_H=Z_{0}\times{}Z_{p}\times{}Z_{e}\). We need to use that \(N_{p}=N_{e}=N_{H}-N_0\). Doing a similar derivations as above, one derives the Saha equation. Again, ionisation is well before \(kT\approx{}\chi\). One consequence of this, is that if one, e.g., wants to know the population in excited states in hydrogen, it is easier to do this relative to the ionised state (since by the time you can excite even to the first excited state with \(\epsilon_2=\chi_H(1-1/4)=10.2\) eV, hydrogen is mostly ionised). For given state \(s\), one thus writes \(n(H_0,s)/n_{p} = (g_s/g_{p}g_{e}n_{e}\lambda_{th}^3)\times\exp((\chi-\epsilon_2)/kT)\).
Finally, back to the chemical potential \(\mu\) (and Baierlein 2001AmJPh..69..423B). In terms of above quantities, one finds \(\mu=\epsilon+kT\log(g\lambda_{th}^3/n)\), but \(\mu\) also enters all thermodynamic potentials (internal energy U, enthalpy H, Helmholtz free energy F, Gibbs free energy G), as an additional term \(\dots+\mu{}dN\), i.e., the energy required to add one particle. In particular, for constant T, V, Helmholtz is handiest: \(F(T,V,N)=PV+\sum_{i}\mu_{i}N_{i}\) (and \(dF=PdV+\sum_{i}\mu_{i}dN_i\)). For pair plasma, minimizing \(F\) for \(N_{+}=N_{-}\) (holding \(T\), \(V\), other \(N\) constant), one requires \(\mu_{+}+\mu_{-}=0\). With the above microscopic definition of \(\mu\), one recovers the solution. Similarly, for ionisation, \(\mu_0=\mu_p+\mu_e\). In general, for any reaction left↔right, one expects that in equilibrium, \(\sum_{\rm left}\mu=\sum_{\rm right}\mu\). (In that sense, the above are missing photons – but these have \(\mu_\gamma=0\).)
All the above was for classical particles, but the same holds for non-classical ones (except of course that one cannot assume a Maxwellian once particles start to overlap, \(\lambda_{th}\approx{}d=n^{-1/3}\)). For completely degenerate neutron gas, where \(\mu=\epsilon_F\), one now trivially finds that there will be a contribution of protons and electrons such that \(\mu_n=\mu_p+\mu_e\). (Here, there is no \(\mu_\nu\), since the neutrinos escape; for a hot proto-neutron star, where the neutrino opacity is still high, one does need to include it.) Remember, however, that above we derive a final, equilibrium state. The process to get there can be slow – not all baryons are in the form of iron yet!
4. Heat loss
Radiative diffusion; conduction; opacity sources; Schwarzschild and Ledoux criteria; mixing length theory; convective flux; stellar context for convection; semi-convection.
Thu Jan 23
- Textbook
- KWW 5.1, 5.2 (latter only briefly discussed in class, do read!), KWW 6 up to 6.5 (AST 320 notes 6)
- Exercises
- Draw for yourself expected trajectories of blobs that were offset for different conditions: stable, convection, semi-convection.
- AST320 mini problem sets: V
- General knowledge question
- Describe the condition for a star’s envelope to become convective. Why are low mass stars convective in their outer envelopes while high mass stars are convective in their inner cores?
Radiative flux: Frad=-(1/3) (c/κρ) dUrad/dr
Like general diffusion equation: j = -(1/3) vl ∇n
Eddington equation: dT/dr = -(3/4ac)(κρ/T3)(l/4πr2)
Rosseland mean: 1/⟨κ⟩ = (π/acT3)∫ν(1/κν)(dBν/dT)dν
Effectively, a weighted average of the transparency.
Criterion for convection: -(1/γ)dlnP/dr > dlnρ/dr
- Schwarzschild criterion
- Ignoring composition gradients → ∇ad<∇rad,
where ∇ad=(dlnT/dlnP)ad=1-1/γ and ∇rad=(dlnT/dr)rad/(dlnP/dr)=(3/16πacG)(κℓP/mT4) - Ledoux criterion
- With composition gradients → ∇ad<∇rad-f∇μ,
where ∇μ=dlnμ/dlnP and f=(∂lnρ/∂lnμ)/(-∂lnρ/∂lnT); f=1 for fully-ionised ideal gas.
Damped and driven oscillation
Damped because of slow thermal adjustment. But can be driven when the gradient is in between the Schwarzschild and Ledoux criteria; see KWW 6.2 and 6.3.
Mon Jan 27
- Textbook
- KWW 6 up to 6.5, 7 (AST 320 notes 6)
- Exercises
- AST320 mini problem sets: V
- General knowledge question
- Describe these important sources of stellar opacity: electron scattering, free-free, bound-free, and the H- ion.
Secular instability
A hotter layer with higher mean molecular weigth on top of another is unstable on the thermal adjustment timescale; see KWW 6.5.
Convective flux
Generally, one can write the flux as, \[ F_{\rm conv} = \rho \overline{v}_{\rm conv} \Delta q = \rho \overline{v}_{\rm conv} c_P \Delta T, \] where \(\overline{v}_{\rm conv}\) is a ``suitable average'' of the convective velocity.
In terms of the gradients, one finds \[ F_{\rm conv} = \rho \overline{v}_{\rm conv} c_P T \frac{\ell_{\rm mix}}{2H_P}\left(\nabla-\nabla_{\rm ad}\right), \] where \(\ell_{\rm mix}\) is the mixing length, usually parametrized as a fraction of the scale height, i.e., \(\ell_{\rm mix}\equiv\alpha_{\rm mix}H_P\), with \(\alpha_{\rm mix}\) the mixing length parameter.
The estimate of \(\overline{v}_{\rm conv}\) is the tricky part. We follow the AST 320 notes and balance buoyancy (\(Vg\Delta\rho=\rho Vg\Delta T/T\)) and friction (\(-A\rho v^2\)); evaluate velocity at \(\ell_{\rm mix}/2\); define \(V/A=\beta\ell_{\rm mix}\), where \(\beta\) is a shape factor; and find \[ v_{\rm conv}^2 = \frac{\beta g}{H_P}\frac{\ell_{\rm mix}^2}{2} \left(\nabla-\nabla_{\rm ad}\right). \] This leads to a convective flux given by \[ F_{\rm conv} = \rho c_P T \alpha_{\rm mix}^2 \sqrt{\frac{\beta g H_P}{8}} \left(\nabla-\nabla_{\rm ad}\right)^{3/2}. \] Fortunately, the difficulty does not matter much: in the interiors of stars, convection is so efficient that the final temperature gradient ends up being essentially the adiabatic one. This is why we can treat completely convection stars as constant-entropy polytropes. But near the atmosphere, this is no longer true.
Thu Jan 30
- Textbook
- KWW 17 (AST 320 notes 5).
- Exercises
- Look at Figures of the opacity (5.1 in the AST 320 notes; 17.5–17.7 in KWW), and check you understand the basic processes responsible for their shape.
- Redo AST320 mini problem sets VI (luminosity of a star), and think through what changes if you assume Kramers-like opacities.
- Do AST320 mini problem sets XI (the first stars), questions 1 and 2 (and think ahead for question 3).
- Read ahead KWW 24 (AST 320 notes 7) on the Hayashi line.
Opacities
As discussed in the short presentations by Nolan and Abigail.
Discussed KWW 17, AST 320 notes 5, including why electron-scattering opacity (in units of area/mass) is independent of density, while most other sources scale with density.
Note that KWW and my AST 320 notes differ on the main scaling of the bound-free opacity. This is because KWW considers the case where it is dominated by hydrogen (for relatively low temperatures), while the AST 320 notes follow Carroll & Ostlie and consider the more relevant regime further inside the star, where hydrogen and helium are completely ionised, so the opacity becomes proportional to the metallicity. Of course, in either case, the opacities are rather approximate – see Fig. 5.2 in the AST 320 notes.
Scalings for conduction
KWW 17.6 is a bit brief and slightly misleading, but notes in the end that the equivalent opacity in strongly degenerate gas scales as \(\kappa_{\rm cond}\propto\rho^{-2}T^{2}\). Here, the more extensive derivation I presented in class, which shows that this is indeed the case.
Generally, the flux is \(F=-\frac13vl\nabla{}U\). It can be separated in different components. For photons, we saw \(U=aT^4\), \(v=c\) and \(l=1/\sigma{}n\) and hence one has \(F=-(4ac/3)(T^3/\sigma{}n)\nabla{}T\). Given the definition of conductivity through \(F=-k\nabla{}T\), one infers an equivalent conductivity \(k_{\gamma}=(4ac/3)(T^3/\sigma{}n)\).
For particles, \(U=\frac32nk_{B}T\) and thus \(F=-\frac13vln\frac32k_{B}\nabla{}T\). Again writing \(l=1/n\sigma\), one finds \(k=\frac12k_{B}(v/\sigma)\). For an ideal, completely ionised gas, \(v\propto{}T^{1/2}\) and \(\sigma\sim{}Z^{2}e^4/(kT)^{2}\propto1/T^2\). Hence, \(k\propto{}T^{5/2}\). In general, with the velocity much less than \(c\) and the cross-section substantially larger than that for photons, conduction is not important.
For degenerate material, we should consider ions and electrons separately. The ions still have very short mean-free path, so do not contribute much. For the electrons, only a small fraction \(kT/E_{F}\) near the Fermi surface carries any heat, i.e., \(U_{e}\sim{}n_{e}(kT/E_F)kT\). But those electrons have velocity depending on density, not temperature. Their mean-free path still is \(l=1/n_{i}\sigma\) (\(n_i\) the ion density), but now \(\sigma\sim{}Z^{2}e^4/E_{F}^{2}\propto{}1/E_{F}^2\), and thus \(k_{e}\propto{}(v/\sigma{}n_{i})n_{e}(k_{B}T/E_{F})\propto{}vE_{F}T\). For non-relativistic electrons, \(v\propto{}\rho^{1/3}\) and \(E_{F}\propto\rho^{2/3}\), so \(k_{e}\propto\rho{}T\). For relativistic particles, \(v\to{}c\) and \(E_{F}\propto\rho^{1/3}\), so \(k_{e}\propto\rho^{1/3}T\).
Writing in terms of an equivalent opacity, \(\kappa=(4ac/3)(T^3/k\rho)\) (see KWW Eq. 5.10), one finds for the ionised ideal gas, the opacity for for non-relativistic degenerate electrons scales as \(\kappa_{e}\propto{}T^2/\rho^2\), recovering what is written in KWW 17.6.
Note that the photon opacity should also be affected by degeneracy, since photons can only interact with electrons near the Fermi surface, so \(l_{\gamma}\sim1/\sigma{}n_{e}(kT/E_{F})\). Equivalently, one can write that, e.g., the effective electron-scattering opacity scales as \(T/E_{F}\propto{}T/\rho^{2/3}\) (non-relativistic) or \(T/\rho^{1/3}\) (relativistic). At high densities, however, electron conduction will still win because of its steeper dependence on ρ.
5. Energy production
Nuclear binding energy; Coulomb barrier; reaction channels (PP, CNO, He and beyond, D/Li burning, s-/r-/p-processes); rates and neutrinos.
Mon Feb 3
- Textbook
- KWW 18.1, 18.5.1 (p-p and CNO cycles). Slowness of p-p compared to Li+p and D+p due to weak reaction. [Parts of AST 320 notes 8]
- Exercises
- AST320 mini-PS XI on the first stars.
- General knowledge questions
- Explain qualitatively why the first step of the p-p chain is much slower than the second.
Tunneling probability
In class, we discussed how one can use the Heisenberg uncertainty principle to derive, roughly, the exponent of the tunneling probability; see KWW, Eq. 18.9.
Thu Feb 6
- Textbook
- KWW 18, including 18.3 and 18.4 (not discussed in class), and 18.7, but not 18.6. [AST 320 notes 8]
- Exercises
- AST320 mini-PS XII (the rather different mass-radius relation for the first stars).
- General knowledge questions
- Why does helium fusion effectively involve 3 alpha particles?
- After Helium fusion, what are the main elements produced?
- (not such "general knowledge") After Helium fusion, what has happened to the original C, N, and O?
EB revisited: ∂l/∂m = ε-εν+εg
Specify contributions from neutrino losses and contraction/expansion.
Neutrino losses were discussed by Mattias in class; they can become significant at high temperature.
More on tunneling
See wiki:Quantum_tunneling; hyperphysics:quantum/barr; similar to wiki:Evanescent_field#Evanescent-wave_coupling relevant for the two-prism example mentioned in class.
See also Michael's python code to simulate tunneling.
Note the link between fusion and radioactivity, discussed by Michael. This was solved by Gamov 1928ZPhy...51..204G (download PDF via UofT library; in German, but perhaps do-able even if you don't know it).
General temperature dependence, and effects of resonances
Generally, we write the cross section \(\sigma(E)=(S(E)/E)\exp(-b/\sqrt{E})\), and integrate over \(E\) to get \(\langle\sigma{}v\rangle\), i.e., \[ \langle\sigma{}v\rangle=\sqrt{\frac{8}{\pi\mu}}\left(\frac{1}{kT}\right)^{3/2} \int_E S(E)\exp(-E/kT-b/\sqrt{E}) dE \] Normally, \(S(E)\) can be taken out of the integral and one finds the Gamov peak, with height \(\exp(-3E_0/kT)\), with \(3E_0/kT=-19.721(\mu/m_u)^{1/3}(Z_{a}Z_{b})^{2/3}T_{7}^{-1/3}\) (here, \(\mu=m_{a}m_{b}/(m_{a}+m_{b})\) is the reduced mass, not the mean molecular weight).
But, as discussed by Joshua, resonances can be important. The above holds if one's energy is in the far wing of a resonance, so that \(S(E)\) indeed varies slowly. But if the resonance is inside the Gamov peak, it can dominate the energy dependence. In that case, one can consider it as a delta function, and the reaction rate will scale just with \(\exp(-E_{res}/kT-b/\sqrt{E_{res}})\), i.e., the only temperature-dependent part comes from how many particles have the right energy. For this reason, the \(3\alpha\) reaction rate has a term with \(\exp(-C/T)\) instead of \(\exp(-C/T^{1/3})\).
Pycnonuclear fusion
As discussed by Sarah, at high density, electron shielding means nuclei start to notice each others repulsion less and less, and the fusion rate starts to depend on density more.
The figure Sarah showed was from my paper on SN Ia progenitors, 2013RSPTA.37120236V. Note the predictions for stable Nickel isotopes I mentioned in class.
6. Evolution of single stars
Mon Feb 10 - Completely convective stars and the pre-main sequence
- Textbook
- KWW 10 (stellar models), 11 (boundary conditions), 24 (Hayashi line) [AST320 notes 7 and 9]
- Exercises
- AST320 mini-PS XII (the rather different mass-radius relation for the first stars).
- Read KWW 12 if you are interested in how one actually constructs numerical models.
- For fun, have a look at a paper by your instructor where the Hayashi line turned out to be important: 2000ApJ...529..428V (and the acknowledgement of the referee).
- General knowledge questions
- In what ways are the first, zero-metallicity stars different from current ones? How does this affect their radii and luminosities?
- What sets the luminosity of a completely convective star?
Thu Feb 13 - evolution towards and on the main sequence
- Textbook
- KWW 28, 30 (29 for interest) [AST320 notes 10, 11].
- Exercises
- Check you understand the qualitative shapes of proto-stellar tracks (KWW Fig. 28.3; AST 320 notes, Fig. 7.3).
- Check that you understand the different ends of the main sequence for different masses listed in AST 320 notes 11, and how these relate to what one sees in the HRD (AST320 notes Fig 10.2 is well worth studying in detail).
Aside: neutrino lines vs continua
A fusion reaction generally creates a lot of energy, \(E_{\rm r}\) which has to be distributed over the output products. If those are just a nucleus and a neutrino, like for the \({}^{7}B(e^{-},\nu)^{7}Li\) reaction, momentum and energy conservation mean that the light particle (the neutrino) will get essentially all the energy (the relevant ratio being \(E_{r}/m_{Li}c^{2}\)). But if also a positron is produced, which has a small rest mass (relative to the energy produced) as well, the energy can be shared between the positron and the neutrino, so one gets a spectrum.
Note that the reasoning is analogous to why electron scattering does not change the energy of the photon much, unless the photon (or electron) energy is of order \(m_{e}c^{2}\); see wiki:Compton_scattering.
Approach to the main sequence
Generally, contract until some fusion process can provide the luminosity radiated. On the way to the main sequence, D and Li are fused, but for most stars, the first fusion stage that can hold up the contraction for a little while is the first part of the CNO cycle, where C is turned into N (see Fig. 7.3 in the AST320 notes). Only when the C is exhausted does the star contract further until either the p-p chain or the full CNO cycle takes over.
On the main sequence
Hydrogen converted to Helium. In low-mass stars, radiative core so centre exhausts first. In more massive stars, convective core exhausts in one go, though the convection zone slowly becomes smaller during the main sequence. In detail, this depends on how convection actually happens, i.e., on overshooting and semi-convection.
For both, the luminosity increases slightly. Qualitatively, one can understand this from the increase in mean molecular weight μ. Naively, one would expect a decrease in radius, but changes in stellar structure counteract this (i.e., the star does not change homologously). Only in the final stages does the radius descrease a little.
End of the main sequence
The core contracts and a shell around it ignites. In general, if a stable core can be formed, it will become isothermal. But there is a maximum (see KWW and AST320 notes); beyond that the core has to contract and either ignite He fusion or become degenerate.
Mon Feb 24 - Giant Branch and Helium Flash
- Textbook
- KWW 33.1–6, AST 320 notes 12, low-mass giants.
- Exercises
- Check that you understand the basic differences between fusion in main-sequence and giant stars, and in degenerate cores.
- Ensure you understand why for low-mass stars, the helium flash happens at a fixed core mass and luminosity, (nearly) independent of the stellar mass.
- Study the figures with evolutionary tracks and perhaps especially Fig. 12.4 in AST 320 notes.
Giant stars
For a sufficiently dilute envelope (M small and/or R large), the properties of shell determined by the core only, as the envelope is all ``far away.'' In particular, kT≈GMcμmH/Rc(HP/Rc), where the ratio of the scale height to the core radius, \(H_{P}/R_{c}\), is constant for homologous stars.
As a consequence, if, e.g., the core contracts, T will go up and so will the luminosity, causing the envelope to expand: mirror principle.
Note the red bump going up the main sequence, a consequence of a downward jump in μ at some point due to the convection having reached partially inside the region in which some fusion has happened. When the shell reaches that point, T will go down a little. See KWW 33.3.
Helium flash
For low-mass stars, the degenerate helium core is at about the same temperature as the shell. Eventually, helium ignites, at a core mass of about 0.45 Mo, somewhat off centre. Since the core is degenerate, a thermonuclear runaway ensues, though it does not become dynamically unstable.
Thu Feb 27 - Intermediate Mass Giants, Blue Loops
- Textbook
- KWW 31, AST 320 notes 12, intermediate-mass giants; also KWW 33.3, about the ``red bump'' for low-mass giants.
- Exercises
- Check you understand what causes the first and second dredge up.
- To better understand the loops, read Lauterborn et al., 1971A%26A....10...97L (for recent discussion on blue loops, see Walmswell et al. 2015MNRAS.447.2951W; for more general insights, Gautchy 2018arXiv181211864G).
- Study the figures with evolutionary tracks and perhaps especially Fig. 31.2 in KWW.
Mon Mar 3 - Asymptotic Giant Branch: Mcore-L relation and superwind
- Textbook
- 34.1 (overview), 34.4 (core-mass lum. relation), AST 320 notes 12 (parts)
- General knowledge questions
- What is Eddington’s luminosity limit?
- Sketch out a Hertsprung-Russell diagram. Indicate where on the main sequence different spectral classes lie. Draw and describe the post main-sequence tracks of both low- and high-mass stars.
Eddington luminosity
I find it easiest to derive from force balance (which makes sense only for optically thin material above a star's photosphere): \[ F_{\rm grav} = -\frac{GM}{R^2}m = F_{\rm rad} = \frac{L}{4\pi{}R^2}\sigma{}N \] where with \(m=\rho{}V\) and \(\sigma{}N=\sigma{}nV=\kappa\rho{}V\), one finds \[ L_{\rm Edd} = \frac{4\pi{}cGM}{\kappa}. \]
End of the AGB
Near the end of the AGB, the luminosity from the shell approaches the Eddington lumnisity relevant for electron-scattering opacity. As a consequence, the core-mass luminosity relation changes from very steep to relatively shallow.
At the cool photosphere, the opacity generally is smaller except when it gets cold enough for dust grains to form. This becomes particularly easy after C has been dredged up. (And pulsations help too.) At that point, the star starts driving a ``superwind'', which removes most of the envelope mass.
Thu Mar 6 - Asymptotic Giant Branch: Shell flashes and Nucleosynthesis
- Textbook
- KWW 34.2 (AGB thermal pulses), 34.5-34.6 (nucleosynthesis; mass loss; white dwarf initial-final mass relation)
- Exercises
- Read also the rest of KWW 34.
- General knowledge questions
- Why is nuclear fusion stable inside a main-sequence star? Under what conditions is nuclear fusion unstable? Give examples of actual objects.
- The so-called r- and s- processes are mechanisms that produce elements heavier than iron. Describe these mechanisms and evidence for them from abundance patterns. Where is the r- process thought to act?
Shell instability (updated Mar 13)
This follows KWW, but somewhat simpler, assuming an ideal gas law, and splitting the process explicitly up in two steps, a first in which some amount of heat is added at constant volume, and then a second in which pressure equilibrium is regained, with the element expanding adiabatically and lifting the envelope homologously with it.
For the first step, adding some extra energy δq at constant volume, i.e., with δρ1=0, one obtains a temperature fluctuation δT1=δq/CV, and an increase in pressure δP1/P=δT1/T
Now the shell will expand with some δρ2/ρ until pressure equilibrium is restored. For an adiabatic change, we have δP2/P=γδρ2/ρ and δT2/T=(γ-1)δρ2/ρ
For an infinitely thin shell, the envelope pressure does not change even as the shell expands, and it is only infinitely little lifted. Hence, for the second change one must have δP2/P = -δP1/P. Thus, one has δρ2/ρ=-(1/γ)δT1/T and δT2/T=-(1-1/γ)δT1/T. Net, therefore, the temperature has not gone down back to what it was: δT = δT1+δT2 = 1/γ δq = δq/γCV. Of course, the latter is just equal to δq/CP, which we could have gotten from the start. Regardless, for this case, the temperaure increases, leading to higher fusion, which leads to further temperature increase, etc., so this is unstable to nuclear runaway.
For a shell with finite width D≪r0, as the shell expands, the envelope will be lifted a little and the envelope pressure will decrease. Assuming homology, δPe/P = -4δR/R = -4δD/r0. At the same time, in the shell δρ2/ρ=δD/D=(r0/D)δD/r0. We now require that δP1+δP2=δPenv and thus δT1/T-γ(r0/D)δD/r0 = -4δD/r0. This implies that δD/r0=δT1/T/(γ(r0/D)-4) and one thus finds δT2/T=-(γ-1)(r0/D)/(γ(r0/D)-4)(δT1/T). With that, δT=(r0/D-4)/(γ(r0/D)-4)δq/CV, i.e., the total temperature change is positive for a sufficiently thin shell, with D<r0/4 (where the exact number is not precise since our derivation assumed D≪r0).
For a central source, one has δρ2/ρ=-3δR/R, and using the same logic one recovers the usual δT=-δq/CV, i.e., the total temperature change is negative.
Mon Mar 10 and Thu Mar 13 - Overall Evolution, Supernovae
- Textbook
- KWW 34.8, 35, 36.1, 36.3 (up to 36.3.4); AST 320 notes 13
- Exercises
- Study both interior (ρ-T) and exterior (T-L) diagrammes in detail,
ensuring you understand the basics. (Further nice ones in the
first
MESApaper: Paxton et al. 2011ApJS..192....3P.) - AST320 mini problem sets: XIII (neutrinos from supernovae)
- Study both interior (ρ-T) and exterior (T-L) diagrammes in detail,
ensuring you understand the basics. (Further nice ones in the
first
7. Binary evolution
Most stars increase in radius as they evolve, often drastically. If in a binary, they may at some point overflow their Roche lobes, leading to mass transfer to the companion. If this is stable, mass transfer will be on the evolutionary timescale. If unstable, it can be on the dynamical or thermal timescale. Masses transfer ceases when the star stops trying to expand; in giants, this is when most of the envelope has been transferred, and the remainder becomes so tenuous that it shrinks. Thus, one generally is left with just the core of the star. This process, and variations on it, is responsible for most of the more interesting stars we observe.
For a general review, see Tauris & Van den Heuvel, 2023pbse.book.....T (available with UofT libraries: Physics of Binary Star Evolution).
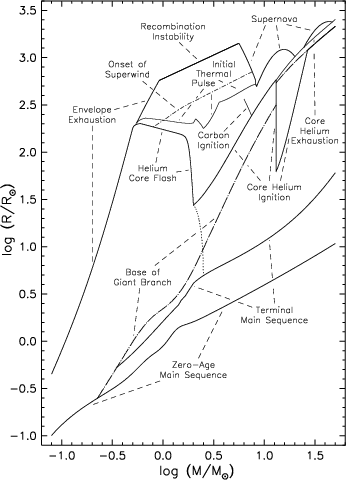
Figure 1: Radius evolution of stars of various masses. Lines indicate properties, as labelled; the one unmarked dotted line between ‘helium core flash’ and ‘core helium ignition’ marks the division between those helium cores (at lower masses) which evolve to degeneracy if stripped of their envelope, and those (at higher masses) which ignite helium non-degenerately and become helium stars. From Webbink 2008ASSL..352..233W, his Fig. 1.
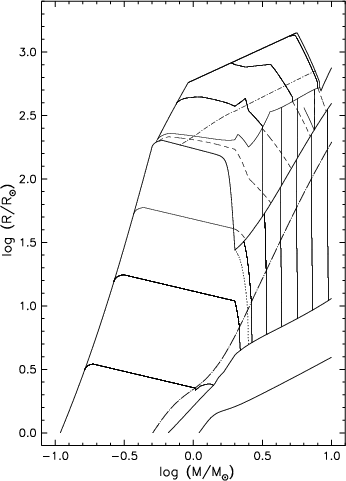
Figure 2: Core masses as a function of radius and mass. Those interior to the hydrogen-burning shell are indicated with solid lines, and dashed lines those interior to the helium-burning shell. Solid lines intersecting the base of the giant branch (dash-dotted curve) correspond to helium core masses of to 0.15, 0.25, 0.35, 0.5, 0.7, 1.0, 1.4, and \(2.0\,M_\odot\); those between helium ignition and the initial thermal pulse to 0.7, 1.0, 1.4, and \(2.0\,M_\odot\), and those beyond the initial thermal pulse to 0.7, 1.0, and \(1.4\,M_\odot\). Dashed lines between helium ignition and initial thermal pulse correspond to carbon-oxygen core masses of 0.35, 0.5, 0.7, 1.0, and 1.4 Mo. Beyond the initial thermal pulse, helium and carbon-oxygen core masses converge, with the second dredge-up phase reducing helium core masses above about \(0.8\,M_\odot\) to the carbon-oxygen core. From Webbink 2008ASSL..352..233W, his Fig. 2.
Mon Mar 17 & Thu Mar 20 - Mass transfer: stability and effects on orbit
Angular momentum loss
Two stars can be driven closer by angular-momentum loss. For gravitational radiation (in a circular orbit), \[ -\frac{\dot J}{J}=\frac{32 G^3}{5c^5}\frac{M_1M_2(M_1+M_2)}{a^4}, \] implying a merger time of \(1.05\times10^7{\rm\,yr}(M/M_\odot)^{-2/3}(\mu/M_\odot)^{-1}(P/{\rm1\,hr})^{8/3}\), where \(\mu=M_1M_2/(M_1+M_2)\) is the reduced mass, and \(P\) the orbital period. Thus, to merge within a Hubble time requires periods less than \(\sim\!0.5{\rm\,d}\).
For binaries with low-mass stars, angular momentum can also be lost by ``magnetic braking'' – a solar-like wind coupled to a magnetic field. This mechanism is usually described by semi-empirical relations, which are calibrated using the rotational evolution of single stars and using population synthesis models for binaries.
Mass loss and tranfer
Consider a star that looses or transfers mass at some rate \(\dot M\).
- Effect on orbit
The angular momentum of an orbit is given by \(J=(M_1M_2/M)\sqrt{GMa}\), and thus, \[ \frac{\dot J}{J} = \frac{\dot M_1}{M_1}+\frac{\dot M_2}{M_2} -\frac{1}{2}\frac{\dot M}{M}+\frac{1}{2}\frac{\dot a}{a} \] With this, we can now consider several cases.
- Conservative mass transfer
Consider mass transfer from star 2 to star 1. If no mass and angular momentum is lost, then \(\dot M_1=-\dot M_2\), \(\dot M=0\), \(\dot J=0\). Thus, \[ \frac{\dot a}{a} = 2\frac{M_{2}-M_{1}}{M_{1}M_2}\dot M_{2} = 2(q-1)\frac{\dot M_{2}}{M_{2}}, \] where \(q=M_2/M_1\) is the mass ratio between the donor (star 2) and the accretor (star 1). For donors less massive than the accretor, the orbit expands upon mass transfer (remember that \(\dot M_{2}<0\)).
Looking at the Roche lobe for a less massive donor, for which \(R_{L}\approx0.46a(M_{2}/M)^{1/3}\), one finds \[ \frac{\dot R_{L}}{R_{L}} = \frac{\dot a}{a} +\frac{1}{3}\frac{\dot M_{2}}{M_{2}} = 2\left(q-\frac{5}{6}\right)\frac{\dot M_{2}}{M_{2}}, \] showing that the Roche lobe, as expected, grows a little slower than the orbital separation. (An analysis valid for all \(q\) would use the approximation of Eggleton 1983ApJ...268..368E, \(R_{L}/a\simeq 0.46q^{2/3}/[0.6q^{2/3}+\ln(1+q^{1/3})]\).)
- Spherically symmetric wind
\(\dot M_{2}=\dot M\), \(\dot M_{1}=0\), \(\dot J=(\dot M_{2}/M_{2})(M_{1}/M)J\). Hence, \[ \frac{\dot a}{a} = 2\left(\frac{M_{1} \dot M}{M_{2}M}-\frac{\dot M}{M_{2}}+\frac{\dot M}{2M}\right) =-\frac{\dot M}{M}. \] Thus, for mass loss (\(\dot M<0\)), the orbit expands.
- Spherically re-emitted wind
\(\dot M_{2}=\dot M\), \(\dot M_{1}=0\), \(\dot J=(\dot M_{2}/M_{1})(M_{2}/M)J\) (idea is that accretor cannot handle mass transferred to it and re-emits it as a wind). Hence, \[ \frac{\dot a}{a} = 2\left(\frac{M_{2}\dot M}{M_{1}M}-\frac{\dot M}{M_{2}}+\frac{\dot M}{2M}\right) =\frac{2q^2-2-q}{1+q}\frac{\dot M}{M}. \] Hence, orbit expands for \(q<(1+\sqrt{17})/4=1.28\) (with again a somewhat lower value for increasing Roche-lobe radius), i.e., it is less quickly unstable than for conservative mass transfer. For a more detailed analysis, see Soberman et al., 1997A&A...327..620S
- Conservative mass transfer
- Effect on stellar radius
If the mass is lost from the outside of a star, the star becomes initially smaller, but on a hydrodynamic timescale it will partially re-expand in responds to the decreased pressure. Which effect dominates depends on the internal structure of the star. Generally, for thermal envelopes, the stars shrinks inside its Roche lobe, re-expanding only on the thermal timescale, typically to nearly its original size (especially for giants). However, a complication for thermal-timescale mass transfer is that, if the secondary is substantially less massive, it cannot accrete sufficiently fast and will bloat itself. For massive stars, this leads to contact, and almost certainly further mass loss and/or a merger. If this can be avoided, then eventually the two stars have equal mass, after which further mass transfer leads to expansion of the orbit, and eventually the donor will regain thermal equilibrium. After that, any further mass transfer is on its evolutionary timescale.
Completely convective stars, or stars with deep convective layers, however, increase in size upon mass loss. For completely convective stars, which are described well by polytropes with \(P=K\rho^\gamma\) with \(\gamma=\frac{5}{3}\) (and thus \(n=1.5\)), this follows immediately from the mass radius relation: \(R\propto{}M^{-1/3}\) (true for constant \(K\), i.e., for constant entropy or completely degenerate, non-relativistic gas). Comparing this to the change in Roche lobe for conservative mass transfer, one sees that stability requires that \[ 2\left(q-\frac{5}{6}\right)<-\frac{1}{3} \Leftrightarrow q<\frac{2}{3}\qquad\hbox{for}\quad n=1.5. \]
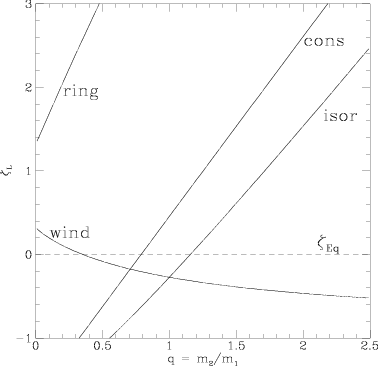
Figure 3: \(\zeta_{\rm L}\equiv\partial\ln R_{\rm L}/\partial\ln M_2\) as a function of mass ratio, with all mass transfer through a single channel: conservative (cons); isotropic wind from donor star (wind); isotropic re-emission of matter, from vicinity of `accreting' star (iso-r). (Also shown is a ring formation, indicative of mass loss from an outer Lagrange point). From Soberman et al., 1997A&A...327..620S, their Fig. 4.
Supernova explosions
One can solve the effect of a spherically symmetric supernova explosion by consiering that, for instantaneous mass loss, the velocities of the two stars remain the same, but their mutual attraction has decreased. Thus, the instantaneous position will become the periastron of the new orbit. For given mass loss ΔM,
\begin{eqnarray} r_{\rm f,peri}=r_{\rm i} &\Leftrightarrow& a_{\rm f}(1-e)=a_{\rm i},\nonumber\\ v_{\rm f,peri}=v_0 &\Leftrightarrow& \frac{G(M_1+M_2-\Delta M)}{a_{\rm f}}\frac{1+e}{1-e}=\frac{G(M_1+M_2)}{a_{\rm i}}.\nonumber \end{eqnarray}Solving this yields \[ e=\frac{\Delta M}{M_1+M_2-\Delta M}, \] i.e., the orbit is unbound if ΔM>½(M1+M2) (as can be seen more easily from the Virial Theorem).
Since the ejecta carry away ΔMv1 in momentum, the binary gets a recoil kick of Δγ to its systemic velocity. The binary's momentum is Δγ(M1+M2-ΔM), so one finds Δγ=-ev1. This one mechanism to cause so-called runaway stars, massive stars (in binaries or not) that are leaving their natal clusters at high velocity. (The other mechanism is N-body interactions.)
Unfortunately, the assumption that supernova explosions are spherically symmetric seems rather poor, since single radio pulsars have large space velocities, of several 100 km/s. As a result, binaries likely unbind even when relatively little mass is lost, and, conversely, may remain bound even if a large amount of mass is lost (indeed, the latter may be a requirement to understand low-mass X-ray binaries, in which neutron stars accrete from low-mass companions). There is fairly strong evidence, however, that some supernovae do not impart (large) kicks, possibly those due to electron capture. For more details, see Tauris & Van den Heuvel, 2023pbse.book.....T, §13.7.