Cookbook on Broadening Function (BF) determination using the SVD technique
Important: The BF method provides superior
resolution and is basically immune to natural broadening of the spectral lines.
Thus, you do not have to remove broadened Balmer lines from A- or F-type
spectra if such broadening is present also in the spectrally matched template;
such lines carry good information on radial velocity. But the method is
EXTREMELY sensitive to the presence of any line emissions which are not present in
the template. If you have emission lines in the program spectra,
you should better cut these parts off and
splice the velocity binned spectra. The emission lines will produce spurious
absorption notches in the BF's.
This "Cookbook" is intentionally rather didactic. If you want
to go straight into the guts of the method, mostly for the specific
spectroscopic setup used by us at the DDO, read the
description for the DDO programme with comments on
the IDL routines. All IDL routines mentioned below are available as
BFall_IDL.pro, a combined file of all routines. In
IDL, open this file and then compile all routines in one go; this may have to
be done several times to re-link routines as they are compiled.
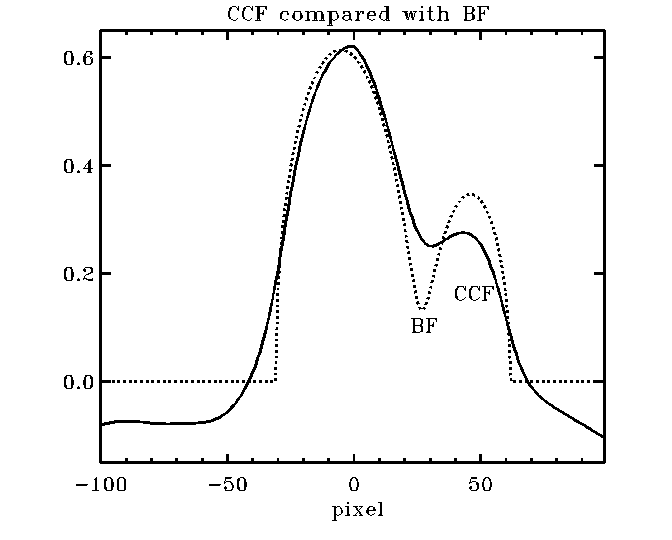 Why to use the BF (broadening
function) rather than CCF (cross-correlation function)? This picture tells the
whole story: The BF is a true linear de-convolution, with the proper baseline
at zero and no distortions, while the CCF is a non-linear
proxy of the BF showing "peak pulling" or "peak pushing away"
effects (due to addition rather than cancellation of common broadening effects
and the interaction with the secondary fringes), funny (i.e. wrong) baseline
and all sorts of distortions that you want to avoid. But, if you are reading
this cookbook, you are probably already convinced ...
Why to use the BF (broadening
function) rather than CCF (cross-correlation function)? This picture tells the
whole story: The BF is a true linear de-convolution, with the proper baseline
at zero and no distortions, while the CCF is a non-linear
proxy of the BF showing "peak pulling" or "peak pushing away"
effects (due to addition rather than cancellation of common broadening effects
and the interaction with the secondary fringes), funny (i.e. wrong) baseline
and all sorts of distortions that you want to avoid. But, if you are reading
this cookbook, you are probably already convinced ...
And now a disclaimer in the normal friendly spirit of software manuals and
books: I assume no responsibility whatsoever for any problems due to my
mistakes or your mistakes ...
If you do use my routines and find them useful, I would
appreciate mentioning this in your publication. The references are:
(AW UMa 1992)
Rucinski, S. M., 1992, AJ, 104, 1968
and
(DDO-7)
Rucinski, S. M., 2002, AJ, 124, 1746.
The following papers may be also useful:
[1]
a pedestrian introduction (from the conference in Izmir, Turkey in 1998),
[2] a
simplified exposition which is shorter than
the lengthy paper [1] and more accessible (Rucinski, S.M. 1999,
IAU Coll.170, "Precise Stellar Radial
Velocities", eds. J.B. Hearnshaw and C.D.Scarfe, ASP Conf.Vol.185, p.82),
[3] a short
note why BF is better than CCF (2004, IAU Symp.215, p.17).
IDL versions: A major change in the array multiplication was
introduced in the Version 4.
The routines below follow the Version 5 conventions and it is best not
to try any earlier version of IDL. IDL is a product of Research Systems Inc.
(now IDL is owned by Excelis Visual Information Solutions)
and is protected by copyright and trademark conventions.
A self-contained Windows application has been written by Bob Nelson.
If you want to avoid IDL, you can copy Bob's ready for use program from BobNelson.zip. I still suggest that you
read the explanations below as the program of Bob
assumes that the reader knows what he/she is doing...
1. Reading in the FITS spectra
Read in your spectra into IDL. Reading in ascii files is part of what is
described in IDL manuals, so I skip that. Routines from the Astro-IDL library are
very useful for FITS spectra (and for ascii tabular data in columns). Pay
special attention to the compatibility of the IDL versions. Since the FITS
standard is not very strict, you may want to try various FITS readers given
there. The routine readfits.pro usually works well, although it is known to
give problems when IDL-4 and IDL-5 versions are mixed up (it uses several other
routines from the IDL-astro package, all must be compatible).
If the standard spectrum is to be called
ss and the program spectra sp1, sp2,...,
read them in as follows (remember that before use, each
routine must be compiled with: .run routine_name - without the .pro extension):
ss=readfits('file-std.fits',hs)
sp1=readfits('file-p1.fits',hp1)
sp2=readfits('file-p2.fits',hp2)
Although the headers do not have to be read with readfits.pro, it is easier
to use the header data contained in simple string arrays, such as
hs, hp1, hp2 in the restoration of the
wavelength scale for each spectrum. In the FITS files, the relevant data are
usually under: CRVAL1 and CDELT1 (starting wavelength and increment). Write
down these numbers for each spectrum (they will be different because of the
heliocentric corrections already applied to the wavelengths) and then create
the wavelength vectors ws, wp1, wp2.
Say, for CRVAL1=5185 and CDELT1=0.0215:
ws = 5185.0 + 0.0215*findgen(1024).
Here 1024 is an example of the actual length in pixels. Usually, it will be the
same as for ss, sp1, sp2 etc.,
but the exactly same length is not crucial because the spectra will be
re-sampled to log(wave) scale anyway. In fact, typical IRAF reductions with
removal of blemishes at ends of the spectra may have resulted in a smaller
number than 512, 1024, 2048, etc, so check the length of
ss, sp1, sp2 using the statement
Help
then make the vectors, sp, w of the same length.
At the end of this step, you should have the data and wavelength vectors for
each spectrum. The headers will not be needed, but you can keep them.
Usually, rectified and normalized spectra are used in the process. This
way one avoids any influence of the sloping continuum. However, for a proper
handling of the ends (where a jump from unity to zero would occur), it is
important to convert spectra to a form in which the absorption lines are
represented by positive spikes. Then the ends are usually close to zero, but
the content is not changed in terms of the usefulness for the de-convolution.
ss=1.-ss
sp1=1.-sp1
sp2=1.-sp2
...
2. Re-sampling to equal velocity (log lambda) steps
Now we will create one vector of wavelengths which will serve all spectra
and will be in equal increments of log lambda.
The pixel spacing determines the velocity spacing, delV. If you take the
high wavelength end of the spectrum and divide CDELT1 by the wavelength at this
point, you will have an optimal spacing. However, any round number will be fine
as long as you sample at a frequency close to or higher than the original
sampling (this will preserve the information content).
Say, you decide on velocity resolution delV=12 km/s. Then you create
one wavelength vector for all spectra, w1:
r = 12.0/2.997924d5
w1 = 5187.0 * (1.d0+r)^dindgen(1024)
r is the inverse of the
spectroscopic resolution power R.
Note that we started at 5187. This was selected to
be a safe, same start for all spectra. Some of them could have the first pixel
at 5185.5 or at 5186.2 (due to heliocentric corrections), so one must check all
spectra where they actually begin and select a good common start. This is an
important step because you are setting the relative velocity scale for all
spectra. The resulting BF will be in relative velocity scale, program star
minus standard (template) star. It may be prudent to check how far the spectra
go, so in this example, check if the last element (in our case:
w1[1023]) is safely within the ranges of
ws, wp1, wp2.
The re-sampling is through a simple linear interpolation:
ssr=interpol(ss,ws,w1)
sp1r=interpol(sp1,wp1,w1)
sp2r=interpol(sp2,wp2,w1)
The size of the vector w1 and
of the re-sampled spectra is called n
in the text. Recall that it is pretty arbitrary and does not have to be 1024 or
anything like that, but should be close to (or slightly larger than) the number
of pixels in the original spectra. For the BF determination as described below
in Sec.4, the number of pixels should be even.
3. Cross-correlation function (CCF)
If you like, you can cross-correlate your spectra to have some idea what is
there. Suppose your span in velocities is 2400 km/s sampled at 12 km/s. Then,
for 201 pixels centred at zero, with 100 elements each way, use:
lag = findgen(201)-100 ; lag vector
ccf1 = c_correlate(ssr,sp1r,lag) ; correlation ssr with sp1r
ccf2 = c_correlate(ssr,sp2r,lag) ; correlation ssr with sp2r
vel = lag*12.
plot,vel,ccf1
Note that the sense of the CCF is: How much to shift the template to fit the
program spectrum, not the reverse...
For many applications, such as single-object radial-velocity determinations,
CCF's are totally adequate and you do not have to go into the pain of the
broadening function derivation (no, it is not a pain, actually a lot of
fun...).
4. Broadening functions, part I: Analysis of the standard spectrum
If you have one standard spectrum, you will have to go through this step
only once. It is prudent to use a few standard spectra with slightly different
spectral types. The S/N should be as high as possible, but if it is not, the
SVD technique will take care of the noise and will attempt to remove it by
telling you this through the plot of the vector of Singular Values,
ww, as below. The determination will be
poorer, of course.
The design matrix, des is
formed using a simple procedure map4.pro
utilizing many internal loops. Typical use is:
des = map4(ssr,201)
The span has been selected again 201 pixels, although it can be any other odd
number. A few cautionary notes are in order here: (1) Running of map4 may take
several minutes even on relatively fast computers, mostly because of the very
inefficient loops within the routine. (2) The resulting BF will be
centered on the zero relative velocity, so that the routine is not very well
suited for handling very large velocity differences which arise when dealing
with PopII objects or red-shifted galaxies. In such situations, one must either
set up a wide window and then accept that the BF will appear at one end of
the velocity range or one must make slightly longer velocity-binned spectra and shift
them relative to the template by a known and fixed number of pixels. (3)
Currently, because of the integer index limitation of the IDL, the routine can
only handle spectra which are shorter than 32,000 pixels. This limitation is
becoming more important with new echelle spectrographs producing very long
spectra. The routine is prohibitively inefficient when the integer indices are
replaced by long integers (type L in IDL).
The map4.pro routine is as follows:
function map4,x,m
; version for IDL 4.0 and higher (SMR Feb.15'97)
; shifts vectors x vertically within m
; for broadening functions
t = 0
n = n_elements(x)
if n gt 32000L then begin
print,'n is too large' & goto,E
end
if (m mod 2) ne 0 then begin
print,'m must be odd' & goto,E
end
if (n mod 2) ne 1 then begin
print,' n must be even' & goto,E
end
t = fltarr(m) # fltarr(n-m+1) ; t(m,n-m)=
; t(small,large-small) dimensions
for j=0,m-1 do $
for i=m/2,n-m/2-1 do t(j,i-m/2)=x(i-j+m/2)
E:
return,t
end
The next step SVD will create 3 arrays, ww, u, v:
svdc,des,ww,u,v,/double
Again, this step may be slow on some computers. It is now essential to
plot ww. It is stored as a vector, but these
are actually diagonal elements of a square array. Because of the very large
range in size of the elements of ww
(most of information about the BF is in the first few elements), the best is to
use the lin-log plot:
plot_io,ww
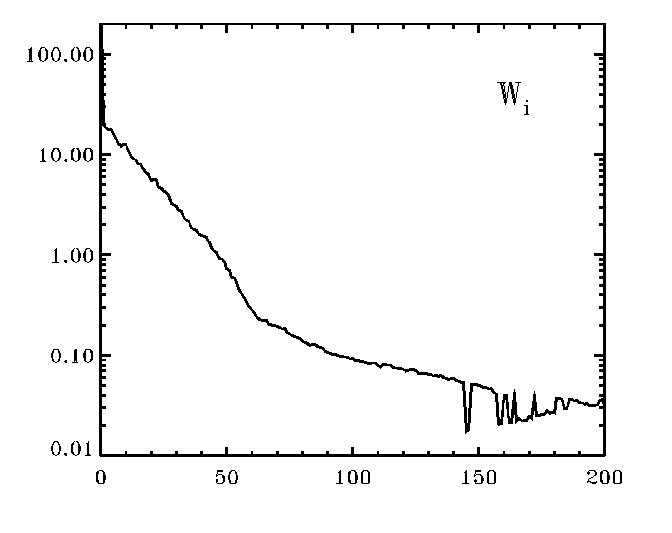 Your plot will look a bit similar to the figure at left.
Note the bends/kinks in the plot. For
the case shown in the figure, you would definitely want to note that the SVD
technique encountered numerical noise at and beyond the index of
ww (=Wi) of about i=140. You
may also suspect, that the kink at about i=65 indicates that (1) the
featureless continuum starts to be represented by these singular values and/or
(2) that the real noise starts to show up about there.
Since the cause (2) depends on
the S/N of the standard spectrum, you can test that.
Your plot will look a bit similar to the figure at left.
Note the bends/kinks in the plot. For
the case shown in the figure, you would definitely want to note that the SVD
technique encountered numerical noise at and beyond the index of
ww (=Wi) of about i=140. You
may also suspect, that the kink at about i=65 indicates that (1) the
featureless continuum starts to be represented by these singular values and/or
(2) that the real noise starts to show up about there.
Since the cause (2) depends on
the S/N of the standard spectrum, you can test that.
Now, the standard spectrum has been resolved into the SVD components.
They will be used to determine the Broadening Functions for program spectra.
5. Broadening functions, part II: Processing of the program spectra
For each program spectrum, you must form its slightly truncated version:
sp1rt = sp1r[201/2:1024-201/2-1]
sp2rt = sp2r[201/2:1024-201/2-1]
I entered the specific numbers for illustration, but you can use a
routine to process these spectra, like the following one:
function trunc,spec,m,n ; must be: m-odd, n-even
return,spec[m/2:n-m/2-1]
end
to be used as:
sp1rt = trunc(sp1r,201,1024)
sp2rt = trunc(sp2r,201,1024)
For each program spectrum, you will form an array of the BF solutions,
say, bb. This can be done using the
following subroutine broadfunct.pro:
pro broadfunct,sp,w,u,v,m,bb
bb=fltarr(m,m)
for i=0,m-1 do begin
wb=fltarr(m)
wb[0:i]=w[0:i]
bb[*,i]=svsol(u,wb,v,sp,/double)
end
return
end
The individual broadening functions can be recovered using:
broadfunct,sp1rt,ww,u,v,201,bb1
broadfunct,sp2rt,ww,u,v,201,bb2
6. Broadening functions, part III: What to do with the broadening function
arrays (Route #1)?
The consecutively better estimates of the broadening functions are the
consecutive rows of the bb1 arrays.
You may want to select the best among them, i.e. giving the most structure, yet
without much of error sneaking in. The last row (in this case bb1[*,200])
gives the full resolution solution, but with all errors.
Note that the elements of this solution are not correlated with each other, with
each point being treated as an unknown. There is no smoothing and no
information on continuity for this last row. But the rows before the last do
show inter-correlation between the elements because some basis functions of the
de-convolution are missing. A description of an alternative approach is given
in Sec.7 below.
So, how far to go? By now we have some idea that, in the specific case as
given above, there is no point of using any of the bb1, bb2
beyond [*,140]; even [*,65] may be suspicious.
Now you can plot these solutions versus the relative velocity
vector:
vel = 12.*(findgen(201) - 100)
(of course, delV=12. may be different in your case):
plot,vel,bb1[*,65]
This will give you a decent result, but this is not the end of the story.
Index 65 is probably still too high. The numerical noise in the SVD
decomposition has been taken care of, but there is still the genuine problem of
the linear dependencies (featureless continuum mapped into featureless
continuum). At this point one may ask: "How many singular values ww[i]
do I need to use for my spectrum?"
Usually, the answer is: "Far fewer than one would imagine".
The proper way is through analysis of the std deviation of the
fit. One should stop at the point where the fit stops improving. If you use too
many ww[i], you just reproduce the noise in the spectrum, not its real shape.
One can use the following routine to obtain the vector sig
representing the error of fit:
function sig,des,bb,sp
m = n_elements(bb[0,*]) ; size of vector
sig=fltarr(m) ; temporary array
pred = des ## transpose(bb) ; predicted spectrum
for i=0,m-1 do sig[i]=sqrt(total((pred[i,*]-sp)^2)/m)
return,sig
end
You would run this function as:
sig1 = sig(des,bb1,sp1rt)
sig2 = sig(des,bb1,sp2rt)
Now check where the error stabilizes. It is important to plot the range from
zero, not over the observed range in y-coordinate, as follows:
plot,sig1,yran=[0,1.1*max(sig1)]
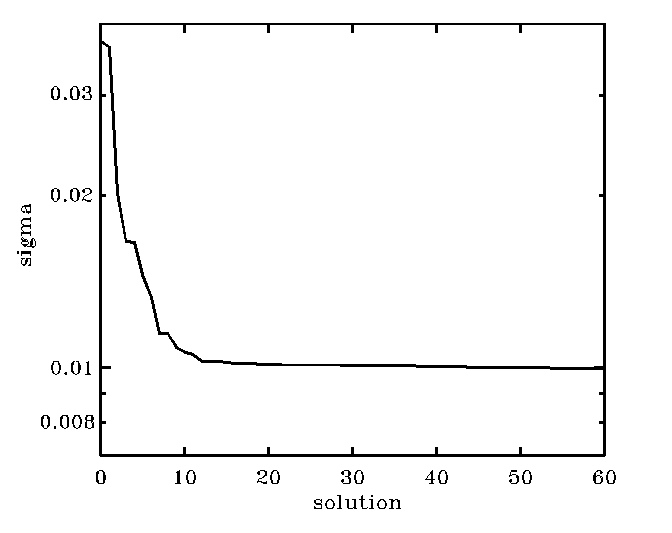 In the case in the figure, the plot suggests that the index as
low as i=15 is sufficiently high
and that bb1[*,15] is a good
solution. This way we would discard some 185 solutions from among 201 solutions
which contain just progressively more noise. If you want to feel better by
seeing some wiggly noise to creep into your results, use bb1[*,20],
but do not go much further than that! A bit of art is involved here...
In the case in the figure, the plot suggests that the index as
low as i=15 is sufficiently high
and that bb1[*,15] is a good
solution. This way we would discard some 185 solutions from among 201 solutions
which contain just progressively more noise. If you want to feel better by
seeing some wiggly noise to creep into your results, use bb1[*,20],
but do not go much further than that! A bit of art is involved here...
The result of the process is a broadening function, say,
bbb=reform(bb1[*,20])
(the IDL command reform
simplifies the vector to strictly 1-D) which may be plotted versus the
velocity vector:
plot,vel,bbb
The function can be used for modeling of the star with spots, for determination
of Vsini or for measurements of radial velocities of components in a binary
system. But this is astrophysics where you know more about the particular
problem so I stop making suggestions here ...
The approach described above, through rejection of - what we
presume - insignificant contributions to BF, will be called here Route#1.
It carries a certain danger for radial-velocity determinations in that the BF's
may be slightly skewed (some basis vectors are rejected). For that reason we, at DDO,
prefer an alternative approach, as described below.
7. The alternative approach (Route#2)
As we said above, no information on continuity of
the BF exists in the last row of the solutions (in our case
bb1[*,200]). All points of the solution are
independent of each other. But one can introduce such correlation between the
elements by choosing a particular solution, say,
bbb=reform(bb[*,20])
This is because many basis functions are then removed and the absolute
independence of the elements of the solution is lost. True, such a solution is
the best you can get to reproduce the observed spectrum, down to the mean
deviation sig. However,
especially for radial velocity applications, when one is ready to accept some
random noise in the BF definition, but would rather prefer not to have any
systematic distortions, you may try a different way...
One can do the following: Select the last row in the broadening-function
array (the full resolution one) and smooth it with a Gaussian. This way you
will be using the powerful property of the full solution that the elements are
totally un-correlated. By smoothing, you remove mostly the un-correlated,
small-scale noise and obtain a better solution. This in fact appears to me a
better approach than removal of many (mathematically seemingly irrelevant)
singular values as their absence may introduce some unwanted systematic
effects. Besides, the instrumental setup usually leads to some local averaging
in the sense that the projection of the spectrograph slit image on the CCD is
usually selected to be of the order of 3 - 5 pixels wide. Any noise at finer scales
must be then caused by the matrix inversion process.
How to do that? Define a smoothing Gaussian with the following function
(you may find more efficient ways, remember hat the Gaussian must be centered
at zero):
function gs_smooth,n,sigma
;
; prepares a n-element vector of total area=1 and Gaussian shape
; given by sigma, shifted to the origin [bbb.....bbb]
; for Gaussian filter using new=cnv(old,gs_smooth)
;
; when a given FWHM needed, use relation: FWHM = 2.354 sigma
; or: sigma = 0.4248 FWHM
b = findgen(n)
c = b
c = ((b - b(n/2))/sigma)^2/2
b(*) = 0.
d = where(c le 30.)
b(d) = exp(-c(d))
b = shift(b, -n/2)
return, b/total(b)
end
You first prepare the smoothing Gaussian (here for sigma = 3.0) and
then use it for smoothing:
gs30 = gs_smooth(201,3.0)
bb30 = cnv(reform(bb[*,200]),gs30)
The convolution can be done using the following compact one-line function
cnv.pro which uses Fourier transforms:
function cnv,a,b
; [SMR: 10 Oct 1992]
; general convolution of two vectors or arrays with same dimensions;
; vector or array b must be symmetric at ends: [bbb........bbb]
; and normalized to integral = 1 (for Gaussians, use gs_smooth for 1-D
; and gs2_smooth for 2-D
;
; usage: new_vector=cnv(vector,smoothing_vector)
;
return,float(fft(fft(a,-1)*fft(b,-1),+1)*float(n_elements(a)))
end
(I prefer this one over the convol.pro
of IDL, although watch at the ends and make sure that spectra go to
zero there).
Which solution is better? Route#1, with the high-order singular values removed
(as in Secs.5 and 6) or Route#2 which uses the full resolution, with the noise
removed by smoothing (as above)? Frankly, I don't know. I hope to find out this
one day... The former is more elegant mathematically, the latter really
guarantees that the result will have no hidden distortions due to missing basis
functions. Both are perfectly legitimate approaches.
8. Fitting Gaussians for binary stars
This is one of specialized applications:
Having the broadening function bbb defined over the velocity
vel, one can determine the binary radial
velocities using Gaussian fits. Note that least-squares Gaussian fits are
usually unstable and that fixing of the widths of the components usually helps.
The four IDL routines are given for
such applications.
Slavek Rucinski. The writeup updated May 2015.
Please let me know if something is unclear or wrong by e-mail:
rucinski@astro.utoronto.ca
 Why to use the BF (broadening
function) rather than CCF (cross-correlation function)? This picture tells the
whole story: The BF is a true linear de-convolution, with the proper baseline
at zero and no distortions, while the CCF is a non-linear
proxy of the BF showing "peak pulling" or "peak pushing away"
effects (due to addition rather than cancellation of common broadening effects
and the interaction with the secondary fringes), funny (i.e. wrong) baseline
and all sorts of distortions that you want to avoid. But, if you are reading
this cookbook, you are probably already convinced ...
Why to use the BF (broadening
function) rather than CCF (cross-correlation function)? This picture tells the
whole story: The BF is a true linear de-convolution, with the proper baseline
at zero and no distortions, while the CCF is a non-linear
proxy of the BF showing "peak pulling" or "peak pushing away"
effects (due to addition rather than cancellation of common broadening effects
and the interaction with the secondary fringes), funny (i.e. wrong) baseline
and all sorts of distortions that you want to avoid. But, if you are reading
this cookbook, you are probably already convinced ...  Your plot will look a bit similar to the figure at left.
Note the bends/kinks in the plot. For
the case shown in the figure, you would definitely want to note that the SVD
technique encountered numerical noise at and beyond the index of
ww (=Wi) of about i=140. You
may also suspect, that the kink at about i=65 indicates that (1) the
featureless continuum starts to be represented by these singular values and/or
(2) that the real noise starts to show up about there.
Since the cause (2) depends on
the S/N of the standard spectrum, you can test that.
Your plot will look a bit similar to the figure at left.
Note the bends/kinks in the plot. For
the case shown in the figure, you would definitely want to note that the SVD
technique encountered numerical noise at and beyond the index of
ww (=Wi) of about i=140. You
may also suspect, that the kink at about i=65 indicates that (1) the
featureless continuum starts to be represented by these singular values and/or
(2) that the real noise starts to show up about there.
Since the cause (2) depends on
the S/N of the standard spectrum, you can test that.  In the case in the figure, the plot suggests that the index as
low as i=15 is sufficiently high
and that bb1[*,15] is a good
solution. This way we would discard some 185 solutions from among 201 solutions
which contain just progressively more noise. If you want to feel better by
seeing some wiggly noise to creep into your results, use bb1[*,20],
but do not go much further than that! A bit of art is involved here...
In the case in the figure, the plot suggests that the index as
low as i=15 is sufficiently high
and that bb1[*,15] is a good
solution. This way we would discard some 185 solutions from among 201 solutions
which contain just progressively more noise. If you want to feel better by
seeing some wiggly noise to creep into your results, use bb1[*,20],
but do not go much further than that! A bit of art is involved here...