Table of Contents
1 Syllabus
- Lectures
- M4, R12, AB 113
- Lecturer
- Marten van Kerkwijk, MP 1203B, 416-946-7288, mhvk@astro.utoronto.ca
- Office hours
- Drop by my office, or by appointment
- Web page
-
http://www.astro.utoronto.ca/~mhvk/TRANSMINI1/ - notes
1.1 Synopsis
Transient stars sometimes appear on the sky. In this course, we will discuss ``transient physics,'' the physics we require to understand known types of transients – novae, kilonovae, supernovae, hypernovae, X-ray and $γ$-ray bursts – and their aftermath. It sets the stage for the companion mini-course where we will compare predicted behaviour with observations. We will also discuss ``predicted transients'' – both those we know must exist and those that seem not impossible (and therefore may well exist – ``everything not forbidden in compulsory'').
1.1.1 Transient Physics
- Known types, basic energetics, scaling relations and timescales.
- Review of relevant stages of stellar and binary evolution.
- Small nuclear runaways: shell flashes and detonations.
- Large nuclear runaways: helium flash, carbon deflagration.
- Removal of pressure support: electron capture, core collapse, pair instability.
- Review of binary evolution, stability of mass transfer.
- Mergers of stars, white dwarfs, and neutron stars.
1.1.2 Course texts
There is no specific book, so we will have to do with review articles, etc. Helpful is a good sense of the structure and evolution of stars and compact objects, ideally through the (equivalent of the) undergraduate course AST 320 or the graduate course AST1410. The book I learned most from is Stellar Structure and Evolution (KW; Kippenhahn & Weigert for first, plus Weiss for second edition; Springer-Verlag, 1990, 2012; for nice and instructive plots, see also the MESA paper, Paxton et al. 2011ApJS..192....3P). For those who did not take undergraduate astrophysics, I strongly recommend An Introduction to Modern Astrophysics, by Carroll & Ostlie (2nd edition; Addison-Wesley, 2006), which introduces more empirical knowledge (and jargon) assumed known in KW. Good too (especially for the sequel) is Supernovae and nucleosynthesis, by Arnett (Princeton Univ. Press, 1996).
1.1.3 Evaluation
- One problem set (pdf), due 2018 Jan 29 (30% total).
- Investigation of a particular type of transient, and discussing this with the instructor (40%).
- Presentation to the class about the transient (30%)
2 Introduction
2.1 What is a transient?
Two possible definitions of an ``interesting'' transient:
- large (>100?) increase in brightness, lasts much less than human lifetime, and recurs infrequently;
- A significant fraction (>1%?) of the total energy available is used in a short time.
One may also want to distinguish between disruption (one-off) and eruption (can repeat).
2.1.1 Known eruptions, bursts, flashes, and flares.
- Failure of hydrostatic equilibrium (HE): Luminous Blue Variable (LBV) eruptions, AGB shells.
- Run-away fusion: shell flashes, Novae, X-ray bursts.
- Magnetic reconnection: M star flares, soft gamma-ray repeaters (SGR), fast radio bursts (FRB)?
- Accretion instability: Dwarf novae, X-ray novae, FU Ori outbursts.
We'll ignore magnetic bursts from here on, as well as the rather common accretion instability transients.
2.1.2 Known disruptions
- Run-away pressure loss: core-collapse SNe.
- Run-away fusion: SN Ia, SN Iax (partial disruption)
- Mergers: (some?) luminous red novae, kilonovae (NS+NS), short gamma-ray bursts (GRB)?
2.1.3 Not yet observed(?) events
Known to occur but not yet(?) observed: helium flash; mergers of different types of objects.
Predicted but not yet(?) observed: in single stars, (pulsational) pair-instability supernovae, carbon deflagration supernovae, electron-capture supernovae; in binaries, accretion-induced collapse of white dwarf to neutron star, accretion-induced collapse of neutron star to black hole (or quark star).
2.2 Basic energetics
2.2.1 Gravitational
\[ E\sim\frac{GM\Delta{}M}{R} = 0.0038{\rm\,B}\frac{M\Delta{}M}{M_\odot^2}\frac{R_\odot}{R} = 500{\rm\,B}\frac{M\Delta{}M}{(1.4\,M_\odot)^2}\frac{10{\rm\,km}}{R}, \] where \(1{\rm\,B}\equiv10^{44}{\rm\,J}\equiv10^{51}{\rm\,erg}\) is the bethe unit of energy (named after Hans Bethe).
Considering the efficiency of generating energy in terms of rest-mass energy, for main-sequence stars (\((M,R)=1\,M_\odot,1\,R_\odot\)), white dwarfs (\(1\,M_\odot,0.01\,R_\odot\)), and neutron stars (\(1.4\,M_\odot,10{\rm\,km}\)), this corresponds to \(GM/Rc^{2}=2\times10^{-6}\), \(2\times10^{-4}\), and \(2\times10^{-1}\).
2.2.2 Nuclear
\[ E\sim \frac{\Delta M}{m_p}Q = 1.9{\rm\,B}\frac{M}{M_\odot}\frac{Q}{1{\rm\,MeV}} \] where \(Q\) is the energy released per nucleon, \(\sim\!7{\rm\,MeV}\) for fusing hydrogen to helium, \(\sim\!1{\rm\,MeV}\) for other reactions. Thus, one gains \(\sim\!7\times10^{-3}\) and \(1\times10^{-3}\Delta M c^2\), respectively.
2.2.3 Comparison with observed energies
The basic energy available is often easy to estimate, though often it has little to do with what we observe directly.
For instance, the total optical light emitted by a supernova is \(\sim\!L\times{}t\sim10^{11}L_{\odot}\times2{\rm\,wk}=0.5{\rm\,B}\) (where I used ``outshines its host galaxy for a few weeks'' in my estimate). This is far less than one would estimate for a core-collapse supernova (most energy is lost in neutrinos). While it is similar to the fusion estimate for type Ia supernovae, for both core-collapse and thermonuclear supernovae, most of the optical light is powered by the radio-active decay of \({\rm^{56}_{28}Ni}\) – so what one really needs is an estimage of its amount (and then use that it provides \(\sim\!1{\rm\,MeV}\)).
Furthermore, some care has to be taken. E.g., a nova shell might ignite when \(\Delta M\simeq10^{-4}\,M_\odot\) has been accreted, which might lead one to estimate \(E\simeq10^{-3}{\rm\,B}\), but in reality much less is emitted: \(\sim L_{\rm Edd}\times1{\rm\,month}\simeq10^{-6}{\rm\,B}\). Radiation does dominates the energetics, but material is ejected before it can be fused.
In constrast, for X-ray bursts on a neutron star, where no matter can leave, the energetics do work: with \(\Delta M\simeq10^{-9}M_\odot{\rm\,yr^{-1}}\times10^4{\rm\,s}\), one predicts \(\sim\!10^{39}{\rm\,erg}\), consistent with the observed \(\sim\!L_{\rm Edd}\times 10{\rm\,s}\).
3 Stability
3.1 Reminder: Basic scalings and timescales
Mass conservation and hydrostatic equilibrium \[ \frac{dM_r}{dr} = 4\pi{}r^{2}\rho \qquad \Rightarrow\qquad \rho\propto\frac{M}{R^3}, \] \[ \frac{dP}{dr} = \frac{GM_{r}\rho}{r^2}\qquad \Rightarrow\qquad P\propto\frac{M^2}{R^4}. \] Dynamical timescale \[ t_{\rm dyn} = \frac{1}{\sqrt{G\rho}}. \]
3.2 Dynamical stability
For a star to be stable to a density perturbation (upon, e.g., compression), pressure has to increase faster than gravity, i.e., faster than \(P\propto{}R^{-4}\).
For a polytrope, \(P\propto\rho^{\gamma}\propto R^{-3\gamma}\), with \(\gamma\equiv{}C_P/C_V\) the adiabatic index (where \(C_P\) and \(C_V\) are the specific heats at constant volume and pressure, resp.). In terms of the degrees of freedom \(f\) of the gas particles, one has \(\gamma=1+2/f\). Hence, for a monatomic ideal gas, one has \(f=3\) for the three spatial motions and \(\gamma=5/3\), for a diatomic one at low enough temperature for vibration not to be important, but the two rotations to be excited, \(f=5\) and \(\gamma=7/5\), and at higher temperature \(f=6\) and \(\gamma=4/3\). One also has \(\gamma=4/3\) for radiation-pressure dominated gas. For degenerate gasses, \(\gamma=5/3\) for the non-relativistic case, \(\gamma=4/3\) for the extremely relativistic case.
Thus, for realistic cases, stars are stable, though they are closer to instability if they are composed of molecules, are radiation dominated, or relativistic. The way to get \(\gamma\) to drop, is ionisation (in its most general form), i.e., let part of the work done compressing matter go into ionisation rather than increasing the kinetic energy of the constituent particles. Examples: molecular dissociation, ionisation, pair creation, and nuclear dissociation. Capture of energetic electrons on protons (to form neutrons and neutrinos, with the latter escaping) has a similar effect.
3.3 Gravothermal specific heat and stability of fusion
For a star to be stable to a temperature perturbation, upon, e.g., an increase in fusion rate, the star has to expand and cool, i.e., have negative gravothermal specific heat (see KW, Ch. 25). For an ideal gas, the virial theorem shows this is the case; for a degenerate gas, though, \(E_{\rm kin}\) (like pressure) does not depend on temperature, and thus fusion is unstable.
Note that if cooling increases with increasing temperature (like for neutrino cooling, but unlike radiative losses), the situation reverses: this is unstable for an ideal gas, stable for a degenerate one.
Another way to understand the stability is by considering the increase in fusion in steps: first, one adds some energy and thus (for a non-degenerate gas) increases the temperature and pressure in some small central region with radius \(r\). Then, the star will expand until the pressure in the central region and that required to support the rest of the star match. For homologous expansion with a fractional change in radius \(\delta{}R\), one gets a final fractional change in pressure \(\delta{}P/P=-4\delta{}R/R=-4\delta{}r/r\). Furthermore, since the mass of the inner region of \(m=\frac{4}{3}\pi{}r^3\) is constant, the density will have changed as \(\delta{}\rho/\rho=-3\delta{}r/r\). Thus, in the inner region, \[ \frac{\delta{}T}{T}=\frac{\delta{}P}{P}-\frac{\delta\rho}{\rho} = -\frac{\delta{}r}{r}. \] Hence, the temperature has decreased relative to the initial state, and thus fusion in cores is stable.
Now consider nuclear fusion in a thin shell around a core with radius \(r\) with thickness \(D\ll{}r\) (think why shells naturally will tend to become thin). Again assume a small increase in energy and thus in pressure and temperature. This will cause expansion of the part of the star above the shell (but not of the core), i.e., some change in radius \(\delta{}R\) until hydrostatic equilibrium has been regained. In the new equilibrium, the pressure that the shell needs to provide will then have been reduced by \(\delta{}P/P=-4\delta{}R/R=-4\delta{}r/r=-4\delta{}D/r\). The difference with the above, however, is the behaviour of the density: the shell has mass \(m\simeq4\pi{}r^{2}D\) and can expand in only one direction, and hence after expansion \(\delta\rho=-\delta{}D/D\). Thus, for a thin shell, the density decreases much faster than the pressure (as, e.g., even a doubling of the thickness of the shell hardly changes the size of the star and thus hardly affects the weight of the layers above). For the temperature, one finds that in the new equilibrium, \[ \frac{\delta{}T}{T}=\frac{\delta{}P}{P}-\frac{\delta\rho}{\rho} = -4\frac{\delta{}D}{r}+\frac{\delta{}D}{D}=\left(1-4\frac{D}{r}\right)\frac{\delta{}D}{D}. \] Hence, in the new equilibrium, the temperature will be above the initial one for \(D < 4/4\). (See KW, §33.2 for more detail.) This instability leads to so-called thermal pulses on the asymptotic giant branch.
4 Basic evolution of stars
Recall the basics of a star's life: to be in hydrostatic equilibrium requires high pressure. For non-degenerate gas, this requires high temperature. High temperature means energy loss, which needs to be compensated either by nuclear fusion or contraction. Since fusion cannot last forever, a star will thus, in the long term, contract. Since \(\rho\propto{}M/R^{3}\) and, in HE, \(P\propto{}M^2/R^4\), one has, for given mass, \(T\propto{}R^{-1}\propto\rho^{1/3}\) both if the pressure is like that of an ideal gas (\(T\propto{}P/\rho\)) and if it is radiative (\(T\propto{}P^{1/4}\)). One sees this behaviour in the schematic tracks shown in Figure 1.
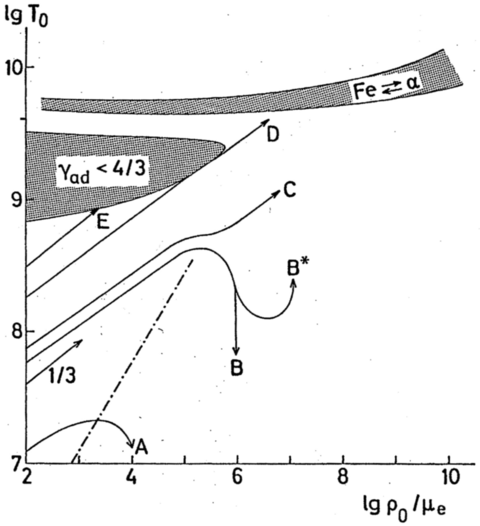
Figure 1: Schematic evolution of the central temperature and density for cores of increasing mass. The dot-dashed line shows the boundary beyond which degeneracy is so strong (and non-relativistic) that contraction leads to a temperature decrease rather than a temperature increase. Track C just misses this as its (core) mass is above the Chandrasekhar mass. Track B* assumes ignition in the degenerate core. Unstable regions are hashed; that due to pair-instability is labeled \(\gamma<4/3\). Taken from KW, their Fig. 34.1.
4.1 Early instabilities
A molecular cloud is roughly isothermal, i.e., \(P\propto\rho\) and thus \(\gamma=1\). Hence, the initial collapse is unstable until the cloud becomes opague and further contraction is adiabatic (with \(\gamma=7/5\) for H2). As H2 is dissociated, and later H ionised, γ drops below \(4/3\) and further collapse occurs.
4.2 Approach to degeneracy
For (cores of) stars below the Chandrasekhar mass (for their \(\mu_e\)), contraction brings them closer to degeneracy – \(P_{\rm ideal}=P_{\rm deg}\) occurs at a line with slope \(T\propto\rho^{2/3}\) since for non-relativistic degenerate gas one has \(P_{\rm deg}\propto\rho^{5/3}\). Once a star becomes degenerate, further loss of energy does not change the pressure or density, but just cools the object.
Above the Chandrasekhar mass, contraction continues to lead to increased heating (see track C in Fig. 1). The separation corresponds to a maximum temperature reachable by a degenerate object of \(1.3\times10^{9}{\rm\,K}\) (for \(\mu_e=2\); see Arnett, §6.1, and Fig. 2).
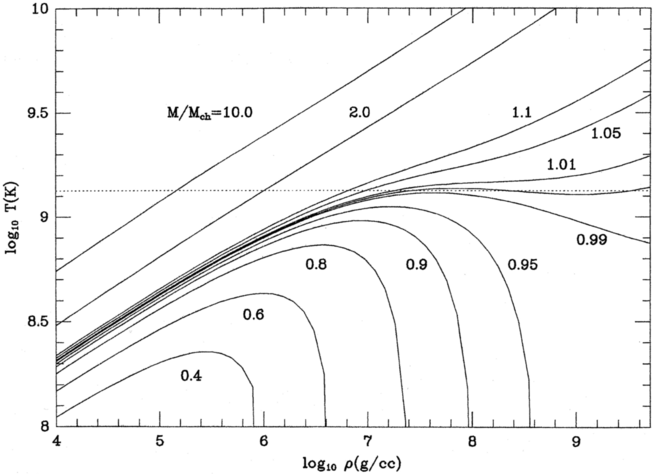
Figure 2: Effects of contraction on temperature and density. From Arnett, his Fig. 6.3.
4.3 Ignition masses
Below the Chandrasekhar mass, the maximum temperature along a track that a star can reach scales with \(M^{4/3}\), and thus for each fusion stage there is a minimum mass – the ignition mass – that determines whether a given (core of a) star can reach it. This is \(\sim\!0.08\,M_\odot\) for hydrogen, \(\sim\!0.3\,M_\odot\) for helium, \(\sim\!0.8\,M_\odot\) for carbon, and \(\sim\!1.36\,M_\odot\) for neon (Nomoto et al. 1984ApJ...277..791N). All heavier fuels are only burnt by stars (or cores of stars) above the Chandrasekhar mass.
In practice, for the helium cores of single stars to contract and ignite directly, requires a main-sequence mass above \(\sim\!2\,M_\odot\) (see Fig. 3), while stars with masses above \(\sim7.5\,M_\odot\) ignite C directly, and stars above \(\sim8\,M_\odot\) ignite all further stages (latter two numbers uncertain).
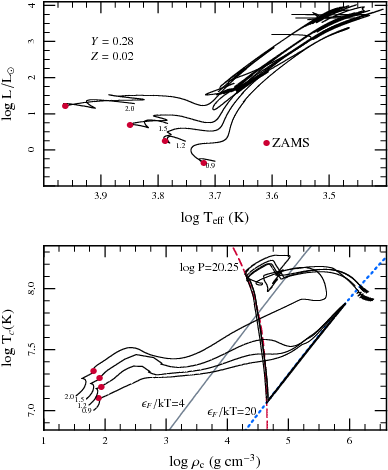
Figure 3: Evolution of low-mass stars. One sees that a \(2\,M_\odot\) can ignite helium under only mildly degenerate conditions, while for lower masses the core density and temperature converge, increasing during the red giant branch up to the helium flash. The flash starts in an outer layer, at \(\rho\simeq4\times10^5{\rm\,g\,cm^{-3}}\), i.e., \(\log\rho\simeq5.6\) (Mocák et al. 2008A&A...490..265M). This is close to where the \(2\,M_\odot\) track takes off and the density and temperature in the shell should evolve similarly. The cores of the lower-mass stars first expand at roughly constant degeneracy (i.e., essentially adjusting adiabatically to the decreasing weight of the overlying layers), before the core is heated such that a run-away occurs. From Paxton et al. 2011ApJS..192....3P, their Fig. 14.
For reference, the burning stages are (from Arnett, his table 6.2):
- Hydrogen burning (\(2\times10^7{\rm\,K}\), \((5\ldots8)\times10^{18}{\rm\,erg\,g^{-1}}\)): mostly helium (via p-p or CNO; all CNO converted to N).
- Helium burning (\(1.5\times10^8{\rm\,K}\), \(7\times10^{17}{\rm\,erg\,g^{-1}}\)): mostly carbon and oxygen (triple alpha, plus \({}^{12}{\rm C}(\alpha,\gamma){}^{16}{\rm O}\), with final abundance ratio strongly dependent on rate, and on extent to which fresh helium is brought in at late stages (which would lead to more oxygen).
- Carbon burning (\(8\times10^8{\rm\,K}\), \(5\times10^{17}{\rm\,erg\,g^{-1}}\)): mainly O, Ne, Mg, Si.
- Neon burning (\(1.5\times10^9{\rm\,K}\), \(1.1\times10^{17}{\rm\,erg\,g^{-1}}\)): mainly O, Mg. Starts with photo-desintegration: \({}^{20}{\rm Ne}(\gamma,\alpha){}^{16}{\rm O}\), followed by \({}^{20}{\rm Ne}(\alpha,\gamma){}^{24}{\rm Mg}\).
- Oxygen burning (\(2\times10^9{\rm\,K}\), \(5\times10^{17}{\rm\,erg\,g^{-1}}\)): mainly Si, S.
- Silicon burning (\(3.5\times10^9{\rm\,K}\), \((0\ldots3)\times10^{17}{\rm\,erg\,g^{-1}}\)): iron-peak.
4.4 Shell burning
In a shell, the density and pressure drop very quickly, and hence their properties depend mostly on the properties of the core. Analogously to main-sequence stars, one can use homology arguments to show how \(\rho\), \(P\), \(T\), and \(L\) scale with \(M_{\rm core}\) and \(R_{\rm core}\). For instance, for the pressure, \[ P \approx \frac{GM_{\rm core}}{R_{\rm core}}\int_{\rm shell}\rho{}dr \approx \frac{GM_{\rm core}}{R_{\rm core}}\rho{}H, \] where homology requires that the scaleheight \(H\propto{}R_{\rm core}\). Here, calculating \(\rho\) requires information on the fusion process and the opacities (for details, see KW, §32.2), but this drops out for the temperature, for which, assuming an ideal gas, one finds \[ T \propto \frac{P}{\rho} \propto \frac{1}{\rho}\frac{GM_{\rm core}}{R_{\rm core}^2}\rho H \propto \frac{M_{\rm core}}{R_{\rm core}}. \] Since fusion is generally a steep function of temperature, this means the luminosity will depend sensitively on the core properties. As the envelopes of red giants are mostly convective, and the photospheres have roughly fixed effective temperature, the radius is also a strong function of core mass.
4.5 Helium flash
The degenerate core will be heated by its surrounding shell, the temperature of which will increase as the core grows in mass and shrinks in size. Furthermore, the contraction will release energy as well. Since degenerate matter conducts efficiently, the core will be nearly isothermal, with a slightly lower temperature in the centre due to neutrino losses (which are stronger at higher density).
When \(M_{\rm core}\simeq0.45\,M_\odot\), the temperature becomes hot enough for ignition, and runaway fusion starts off-centre. This region is only moderately degenerate, which limits the maximum temperature and luminosity reached and thus avoids a dynamic event (timescales for entropy increase always remain larger than the dynamical timescale). In the end, the star settles down as a core-helium burning giant, with most of the luminosity still due to the hydrogen shell. See Fig. 4 for an overview. We see such sources as red-clump stars in metal-rich populations, and horizontal-branch stars in metal-poor ones.
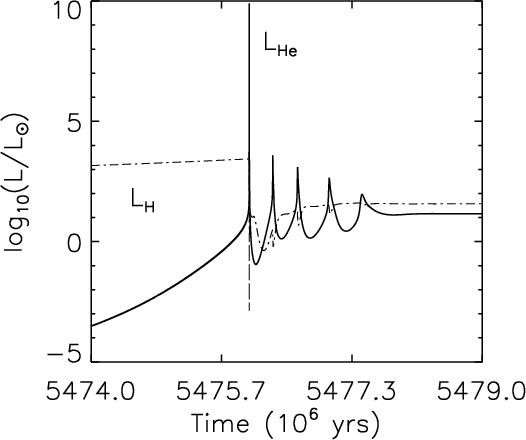
Figure 4: Luminosities during the helium flash. The initial spike is due to the off-centre helium flash. Subsequent spikes occur when inner layers are heated up sufficiently to ignite. As the core is expanding, these reach less high temperatures and luminosities. Note how the luminosity from the hydrogen shell varies in the opposite sense of the helium luminosity. Taken from Mocák et al. 2008A&A...490..265M, their Fig. 4.
4.6 Double-shell burning
When two or more shells are present, they do not necessarily evolve at the same rate, leading to changing separation (in mass coordinates), and to thin shells that are geometrically unstable (see above). This underlies the thermal pulses on the asymptotic giant branch (see Fig. 5).
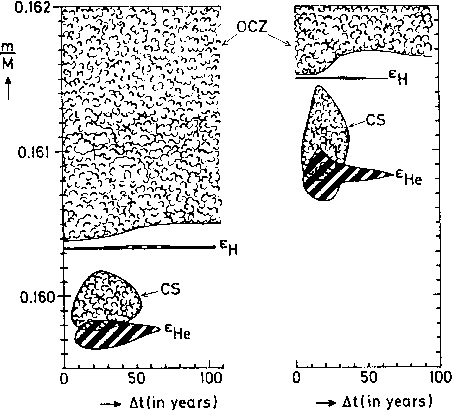
Figure 5: Evolution of the mass shells around the two shell sources in a \(5\,M_\odot\) star near the maximum of the first and sixth thermal pulses. From KW, Fig. 33.4.
4.7 The Carbon flash (that doesn't happen)
Absent mass loss, for a sufficiently massive star, eventually the core density and temperature would increase sufficiently to ignite carbon. This happens as one approaches the Chandrasekhar mass, and in the core, which has a lower ignition temperature due to its very high density (note that the competition between neutrino cooling and compressional heating also makes the temperature distribution less uniform than was the case for a helium core). As one is at very high degeneracy, the run-away destroys the whole core (and surrounding envelope). In reality, this does not happen as the luminosity becomes so high that mass is lost in the AGB super wind.
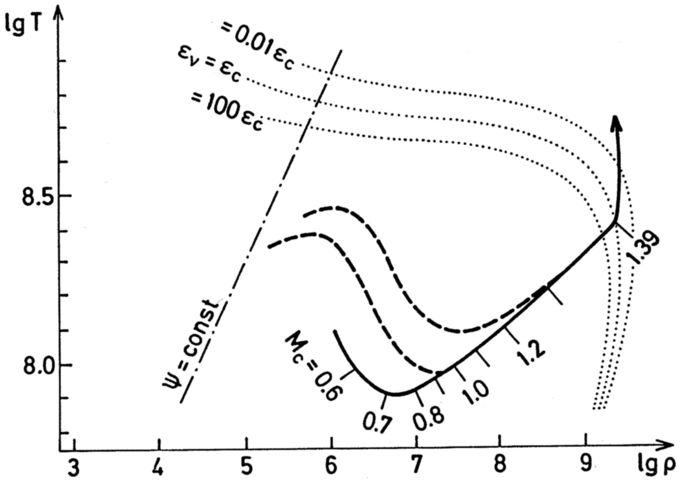
Figure 6: Temperature and density in the CO core of a \(3\,M_\odot\) star after central helium burning. The broken lines show temperature stratifications at two instances. The core grows until carbon is ignited. In real stars, mass loss prevents the core from becoming this massive.
5 Runaway fusion in degenerate cores
Fusion is generally unstable in degenerate cores, as an increase in temperature does not lead to an increase in pressure that leads to expansion and thus cooling. The increased heat will soon lead to convection (see Fig. 7 for the case of the helium flash). The convection zone can extend over a large fraction of the star, and the net effect is that the core moves along a track opposite of that of a contracting star (see Fig. 2): its temperature increases until degeneracy is lifted and the star starts to expand. Whether or not anything dynamic will happen depends on whether burning becomes dynamic before the temperature maximum is reached. If this is not the case, one ends up with a stably burning star.
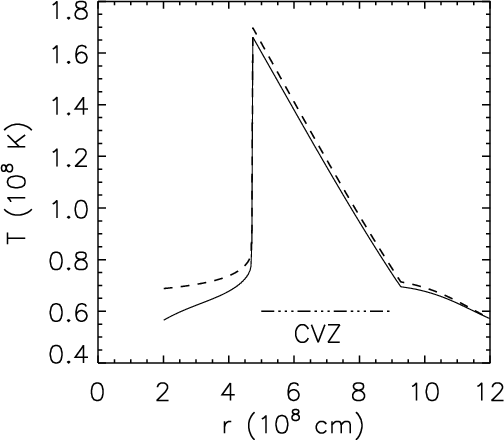
Figure 7: Temperature profile during the initial, off-centre helium flash. Convection ensures that heat is carried out from the burning region. From Mocák et al. 2008A&A...490..265M, their Fig. 2.
5.1 Heating timescale
The local heating time is given by: \[ t_{\rm h,local} = \frac{c_{P}T}{\epsilon}. \] The convection zone, however, will carry away heat to the surroundings, and the temperature will thus increases on a slower timescale, of \[ t_{\rm h, cvz} = \frac{\int_{\rm cvz} c_{P}T dm}{\int \epsilon dm} \approx \frac{M_{\rm cvz}}{M_{\rm fusion}} t_{\rm h, local}, \] where \(dm=4\pi{}r^{2}\rho{}dr\) and \(\int\epsilon{}dm\) is the luminosity \(L\). Given the strong temperature-dependence of fusion, the ratio of masses is typically large, at least ten.
5.2 Local runaway
A fusing region will truly run away either when the convection can no longer carry away the heat sufficiently efficiently, or when a blob passing through the burning region increases its heat faster than it is cooled by rising to a region of lower pressure. In non-degenerate matter, these two conditions give about the same answer, that this happens when the convective velocities approach the velocity of sound, but for degenerate matter where the velocities are lower, the second condition is satisfied first. This happens when along the path, the integral \[ \int_{\rm path} \left[\left.\frac{dT}{dr}\right|_{\rm ad} + \frac{\epsilon}{c_{P}v_{\rm conv}}\right] dr, \] diverges. Approximating crudely, this happens when \[ \frac{\Delta{}T}{\Delta{}R} < \frac{\epsilon}{c_{P}v_{\rm conv}} \qquad \Rightarrow \qquad \frac{c_{P}\Delta{}T}{\epsilon} < \frac{\Delta{}R}{v_{\rm conv}}. \] where \(\Delta{}R\) is the size of the burning region and \(\Delta{}T\) the associated temperature difference. The first term is similar to the local heating time, and the second is the crossing time through the burning region. Hence, a sufficient condition is that \[ t_{\rm h, local} < t_{\rm cross}. \] In practice, run-away will happen earlier, since there will be a distribution of bubbles, some of which will already be a little hotter or move more slowly. For details, see Woosley et al. 2004ApJ...607..921W.
5.3 Deflagration or detonation
Once small region runs away, it initially keeps on rising. It just expands as it is heated until \(t_{\rm heat} > t_{\rm dyn}\), when a flame is born. Its overpressure will not be that high: at \(\rho=10^{9}{\rm\,g/cm^3}\), the Fermi energy is \(\epsilon_F=cp_F=ch(3\rho/(4\pi{}g\mu_e))^{1/3}\simeq4{\rm\,MeV}\), while the burning releases about 1 MeV/nucleon, or about 2 MeV/electron. Hence, at least initially a deflagration front is born, in which the now very hot bubble will ignite neighbouring material by thermal conduction. The speed at which the burning front proceeds is sub-sonic.
To trigger a detonation does not appear to be easy. One way is to have a temperature gradient in which the phase speed at which neighbouring regions run away, \(v_{\rm phase}=(d\tau/dr)^{-1}\), is comparable to the sound speed. For a nice description, see Seitenzahl et al. 2009ApJ...696..515S.
5.3.1 Deflagrations
In a deflagration, the initial bubble and its surroundings can expand, hence become less dense, and thus continue to rise. As they do, the burning region increases in size and becomes somewhat mushroom shaped. If nothing else happens, it will eventually break out, spilling highly processed material into space.
In detail, what happens will depend on the number of sites that can ignite at the same time, and their locations. E.g., if the very centre ignited, the whole white dwarf would be consumed.
Furthermore, it is speculated that the deflagration transitions to a detonation somewhere along the way, when the heat deposited by the deflagration has already substantially expanded the white dwarf.
5.3.2 Detonations
Outcomes are easier to calculate for a detonation: since this propagates supersonically, any given element of the white dwarf will be unperturbed until the shock wave hits it, and will burn to an extent that only depends on its local conditions, which, for degerate parts, means essentially only its composition and density. In Fig. 8 and 9 one sees this for both C/O and He.
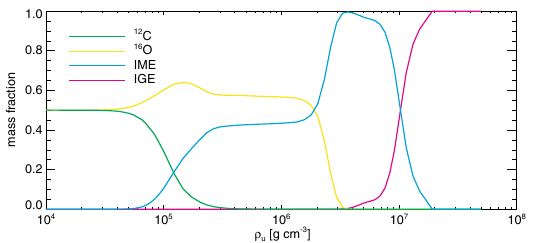
Figure 8: Elements produced by burning degenerate C/O material at different densities. From Fink et al. 2010A&A...514A..53F, their Fig. A.1.
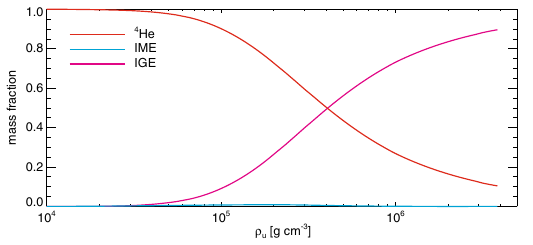
Figure 9: Elements produced by burning degenerate He material at different densities. From Fink et al. 2010A&A...514A..53F, their Fig. A.2. Note how, given the presence of \(\alpha\) particles, any carbon produced in the triple-\(\alpha\) reaction is almost instantly turned into iron-group elements.
5.4 Fusion products
If reactions are sufficiently fast, as in a detonation, there is no time for weak reactions and thus proton and neutron number are conserved separately. Hence, the initial \(\rm^{12}_{6}C\) and \(\rm^{16}_{8}O\) end up in the most stable element with equal numbers of protons and neutrons, \(\rm^{56}_{28}Ni\). Only subsequently does this decay, via \[ \rm^{56}_{28}Ni \rightarrow \rm^{56}_{27}Co + e^{+} + \nu_e \qquad (\tau_{1/2}=6.077~d) \] \[ \rm^{56}_{27}Co \rightarrow \rm^{56}_{26}Fe + e^{+} + \nu_e \qquad (\tau_{1/2}=77.27~d) \] These decays power the lightcurves of most supernovae. Note that there are also gamma rays emitted, as the decays leave the daughter nuclei in excited states.
In contrast, in a slow deflagration, there is time for electon captures (remember that the Fermi energy is very high) and hence in the densest regions one forms stable elements with one proton turned into a neutron, in particular \(\rm^{58}_{28}Ni\) and \(\rm^{54}_{26}Fe\).
For a detonation, all one has is the excess number of neutrons initially present. This is turn depends on the amount of C, N, and O, that the star initially had, as one can see from considering the H and He burning cycles:
H burning: all H to He, (essentially) all C, N, O to \(\rm^{14}_{7}N\) (since the proton capture on \(\rm^{14}_{7}N\) is the slowest step).
He burning: all He to C, O; but also \[ \rm^{14}_{7}N(\alpha,\gamma)^{18}_{9}F(e^{-},\nu)^{18}_{8}O(\alpha,\gamma)^{22}_{10}Ne \] Here, the electron capture (or inverse β decay) of fluorine produces an extra neutron. During a detonation, the \(\rm^{22}_{10}Ne\) would be turned into \(\rm^{58}_{28}Ni\) and \(\rm^{54}_{26}Fe\). Hence, a prediction of detonating little-processed white dwarfs is that the amount of stable nickel should be proportional to the initial metallicity.
In detail, the neutronisation is also affected by the simmering. See, e.g., Chamulak et al. 2008ApJ...677..160C.
6 Electron-capture induced supernovae
For masses above \(\sim8\,M_\odot\) (the mass is uncertain and depends on assumptions about convection, overshoot, etc.), upon helium exhaustian, a sufficiently massive carbon core (at least \(\sim0.8\,M_\odot\), see 4.3) is formed that carbon is ignited before the core becomes degenerate. Carbon fusion leaves a core composed of mostly oxygen and neon. If this core becomes degenerate before neon ignition, the star becomes a ``super AGB'' star.
The further evolution of degenerate ONe cores depends on how much their mass can be increased. If sufficiently close to the Chandrasekhar mass, it could reach densities high enough for the next fusion stage. Unlike for CO cores, however, electron captures start to occur before the density becomes high enough to ignite neon or oxygen burning, which will lead to collapse. In particular, \[ \rm^{24}_{12}Mg(e^{-},\nu)^{24}_{11}Na \qquad (\rho_{\rm crit}=3.7\times10^{9}\;g/cm^{3}), \] \[ \rm^{24}_{11}Na(e^{-},\nu)^{24}_{10}Ne \qquad (\rho_{\rm crit}=5\times10^{9}\;g/cm^{3}), \] \[ \rm^{20}_{10}Ne(e^{-},\nu)^{20}_{9}F(e^{-},\nu)^{20}_{8}O \qquad (\rho_{\rm crit}=9\times10^{9}\;g/cm^{3}). \] Oxygen burning only starts as the core is already irreverably collapsing, launching a deflagration at \(\rho\simeq2.4\times10^{10}{\rm\,g/cm^{3}}\) (Nomoto 1987ApJ...322..206N); see Figs. 10 and 11.
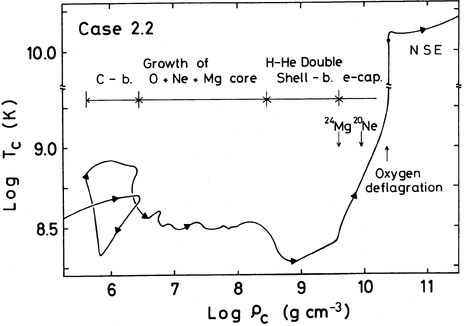
Figure 10: Evolution of central density and temperature of a ONe core that is growing in size (left), and evolution during collapse due to electron captures (right). From Nomoto (1987ApJ...322..206N), his Fig.~4.
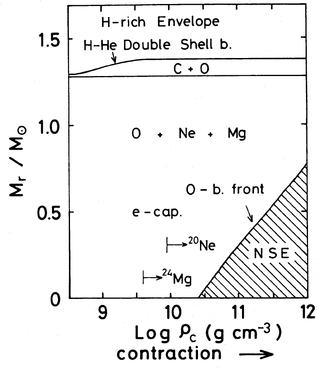
Figure 11: Evolution of the burning front as the core contracts due to electron captures. From Nomoto (1987ApJ...322..206N), his Fig.~6.
In single stars, electron-capture supernovae appear unlikely: after core helium exhaustian and subsequent core contraction, the envelope expands greatly and so does the extent which is convective. For relatively low masses, this enters and removes the outer parts of the helium core (see Figs. 12–15). As a result, for those, the cores are left are too small to grow to the Chandrasekhar mass and will not collapse, while those untouched are so massive that they do not become degenerate at all and evolve up to iron cores and core-collapse supernovae. It appears that only in binaries, with timely removal of the hydrogen envelope, electron-capture supernovae are likely (Podsiadlowski et al. 2004ApJ...612.1044P).
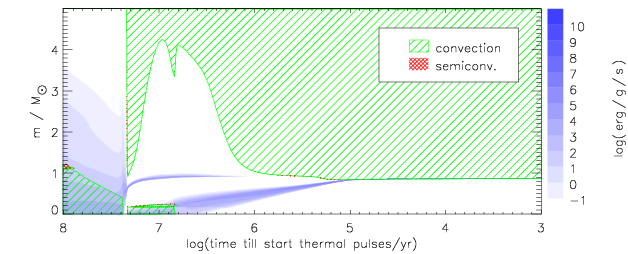
Figure 12: Time evolution for a star with a mass of \(5\,M_\odot\). A small second dredge-up up occurs near \(\log t=5.2\). Taken from Fig. 1 of Poelarends et al. 2008ApJ...675..614P.

Figure 13: As 12, but for a mass of \(11.5\,M_\odot\), for which the dredge-up greatly reduces the helium core mass, ensuring the star ends its life as a ONe white dwarf.

Figure 14: As 12, but for a mass of \(16\,M_\odot\), for which no dredge-up occurs, and hence the core stays well above the Chandrasekhar mass and never becomes degenerate.
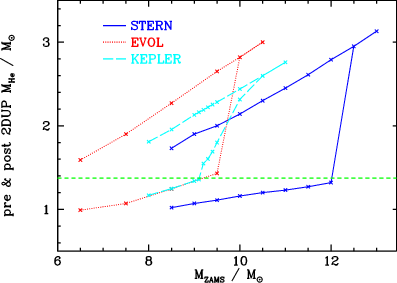
Figure 15: Helium core mass as a function of initial mass for different stellar evolution codes, showing the effects of second dredge-up. Taken from Poelarends et al. 2008ApJ...675..614P, their Fig.~2.