AST 3010: Advanced Topics in Stellar
AST 3010: Advanced Topics in Stellar Astronomy (2011)
Transients
| Lectures | Tuesdays 3 PM and Thursdays 1 PM in AB 113 (first class Th, Jan 13). |
| Lecturer | Marten van Kerkwijk, MP 1203B, 416-946-7288, mhvk@astro
(utoronto.ca) |
| Office hours | TBD (likely after each class, or by appointment) |
| Web page | http://www.astro.utoronto.ca/~mhvk/AST3010/
|
| notes | pdf
|
Synopsis
Transient stars sometimes appear on the sky. In this course, we will
first discuss "transient physics," the physics we require to
understand known types of transients - novae, supernovae, X-ray and
γ-ray bursts - and their aftermath, comparing predicted
behaviour with observations. Next, we will turn to "possible
transients," systematically exploring what systems could lead to
transients, discussing which ones might have possible observational
counterparts, and determining how these could be found by the current
and next generations of transients surveys. The goal is to produce a
complete review of what one might expect, at a level that is useful
for transient surveys, and ideally is suitable for publication (if so,
by the class as a whole; surprisingly, such a review of expected types
of transients does not yet seem to exist).
Transient Physics
- Small Nuclear Runaways: Shell Flashes and Detonations
- Large Nuclear Runaways: He Flash, Carbon Deflagration.
- Sudden Removal of Pressure Support: Electron Capture, Core
Collapse, Pair Instability.
- Mergers: Stars, White Dwarfs, and Neutron Stars
- Evolution of Ejecta: Expansion and Radioactive Heating
We'll start with an overview, then go through the evolution of low,
intermediate, and high-mass stars, briefly discuss binary evolution,
and end with a discussion of lightcurves.
Possible Transients
We will explore systematically what types of transients one might
expect from single stars, binaries, and clusters of stars. We will
focus on binaries, checking for any sensible combination of two types
of stars how they could interact during their evolution, and what
final product one might expect. For a rough sense of the aim, see the
outcome
grid made by Stephen Justham (KIAA/Beijing).
Course texts
Hopefully, there will be a course text by the end! In the meantime,
we will have to do with review articles, etc. What will be important
is to bring a good sense of the structure and evolution of stars and
compact objects. Minimum pre-requisite is the (equivalent of the)
undergraduate course
AST 320; better,
AST
1410 (offered this Fall); see that
course
web page for suggestions for books (personally, I learned most from
Stellar Structure and Evolution, by Kippenhahn & Weigert
[Springer-Verlag, 1990]; also good is Supernovae &
nucleosynthesis, by Arnett [Princeton Univ. Press, 1996]).
Evaluation
Problem sets and mini-research studies (60%), oral presentations
(20%), oral exam (20%).
Mini Research Projects
All students will investigate some particular types of systems (say, a
ONe core white dwarf with a He core white dwarf companion),
research what sort of transients these might produce, write up the
results, and present them in class.
Practically, I hope to divide ourselves in three groups, on white
dwarfs (accreting and merging), main-sequence/giant stars (including
mergers with white dwarfs), and neutron stars/black holes (including
mergers with other types). I would be part of all groups. A growing
list of source combinations and links to references can be found at
types.html.
For each specific topic, I'd hope to proceed as follows:
- Research and write up draft.
- Circulate among group for comments.
- Circulate among class and present (probably best on the board).
- Include further comments in final version.
1 Introduction
What is a transient?
Two possible definitions of an "interesting" transient: (1) large
( > 100?) increase in brightness, lasts much less than human
lifetime, and recurs infrequently; (2) A significant fraction
( > 1 %?) of the total energy available is used in a short time.
One may also want to distinguish between disruption (one-off) and
eruption (can repeat).
Known eruptions, bursts, flashes, and flares
- Failure of hydrostatic equilibrium (HE): Luminous Blue Variable (LBV) eruptions, AGB shells
- Run-away fusion: shell flashes, Novae, X-ray bursts.
- Magnetic reconnection: M star flares, soft gamma-ray repeaters
(SGR).
- Accretion instability: Dwarf novae, X-ray novae, FU Ori outbursts.
Known to occur but not yet(?) observed: helium flash.
We'll ignore magnetic bursts from here on.
Known disruptions
- Failure of HE: core-collapse SNe.
- Run-away fusion: SN Ia.
- Mergers: (some?) luminous red novae, short gamma-ray bursts
(GRB)?
Known to occur but not yet(?) observed: mergers of different types of
objects.
Predicted but not yet(?) observed: in single stars, pair-instability
supernovae, carbon deflagration supernovae, electron-capture
supernovae; in binaries, accretion-induced collapse of white dwarf to
neutron star, accretion-induced collapse of neutron star to black hole
(or quark star).
Basic energetics
Gravitational
For main-sequence stars ((M,R)=1 M☉,1 R☉), white dwarfs
(1 M☉,0.01 R☉), and neutron stars
(1.4 M☉,10 km), this corresponds to ∼ 2×10−6,
2×10−4, and 2×10−1∆M c2.
Core-collapse supernovae and neutron-star mergers :
∼ 1053.5 erg.
Main-sequence mergers : ∼ 1048.5 erg.
Luminous Blue Variable (M=50 M☉, ∆M=1 M☉, R=50 R☉): ∼ 1048.5 erg.
Accretion burst (∆M=· Mt ≅ 10−8M☉ yr−1×10−1 yr):
∼ 1044.5 erg for NS, ∼ 1041.5 for WD.
Nuclear
where Q is the energy released per nucleon, ∼ 7 MeV for
fusing hydrogen to helium, ∼ 1 MeV for other reactions.
Thus, one gains ∼ 7×10−3 and 1×10−3∆Mc2, respectively.
SN Ia : ∼ 1051.5 erg.
Novae : One might think ∆M ≅ 10−4 M☉,
hence E ≅ 1048 erg, but in reality much less is emitted:
∼ LEdd×10−1 yr ≅ 1045 erg
(radiation dominates the energetics). Material is ejected before it
can be fused.
X-ray bursts (∆M ≅ 10−9M☉ yr−1×104 s):
∼ 1039 erg (now consistent with ∼ L Edd×10 s; no mass leaves the neutron star).
2 Stability
Dynamical stability
For a star to be stable to a density perturbation (upon, e.g.,
compression), pressure has to increase faster than gravity. For a
polytrope, P ∝ ρΓ ∝ R−3Γ, with
Γ = ([5/3],[4/3]) for the simplest non-relativistic
and relativistic cases. For a star in hydrostatic equilibrium,
P ∝ R−4. Hence, stability requires Γ ≥ [4/3]
(for a star not described by a polytrope, a suitable average of
Γ).
Ionisation in its most general form causes Γ to drop (the
work compressing matter goes into ionisation rather than increasing
the kinetic energy of the constituent particles). Examples: molecular
dissociation, ionisation, pair creation, and nuclear dissociation.
Capture of energetic electrons on protons (to form neutrons) has a
similar effect.
Gravothermal specific heat
For a star to be stable to a temperature perturbation, upon, e.g., an
increase in fusion rate, the star has to expand and cool, i.e., have
negative gravothermal specific heat (see KW, Ch. 25). For an ideal
gas, the virial theorem shows this is the case; for a degenerate gas,
though, Ekin (like pressure) does not depend on temperature.
Note that if cooling increases with increasing temperature (like for
neutrino cooling, but unlike radiative losses), the situation
reverses: this is unstable for an ideal gas, stable for a degenerate
one.
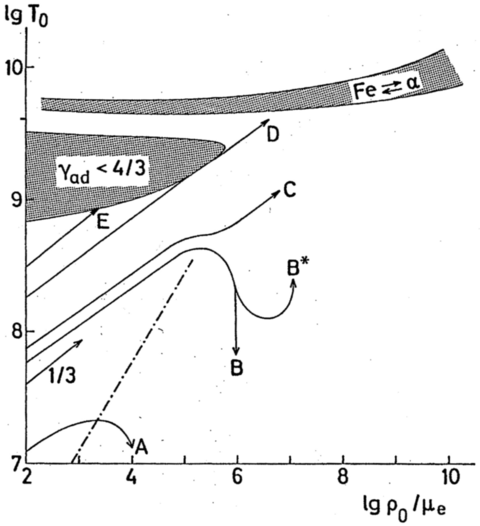
Figure 2.1: Schematic evolution of the central temperature and
density for different core masses. The dot-dashed line shows the
boundary beyond which degeneracy is so strong (and
non-relativistic) that contraction leads to a temperature decrease
rather than a temperature increase. Unstable regions are hashed;
that due to pair-instability is labeled γ < 4/3. Taken from
KW, their Fig. 34.1.
3 Stability of fusion
For a non-degenerate gas, fusion is stable since a small increase in
temperature and hence fusion rate leads to expansion and net cooling
of the core (negative heat capacity). This can be seen from the
virial theorem, or by considering homologous expansion: suppose one
increases the temperature and thus pressure in some small central
region. Then, the star will expand until the pressure in the central
region and that required to support the rest of the star match. For
homologous expansion, one has δP/P=−4δR/R, and hence in
the inner region, δT/T=δP/P−δρ/ρ = −δR/R
(where δρ/ρ = −3δR/R). Hence, fusion in cores is
stable.
Now consider nuclear fusion in a thin shell around a core with radius
r with thickness D << r (think why shells naturally will tend to
become thin). The difference with the above is that now in the shell,
which has mass m ≅ πr2 D, δρ = −δD/D=−(r/D)δr/r, while the weight to be carried and thus the
pressure still scale as δP/P=−4δr/r. Hence, for
expansion of a thin shell, the density decreases but the weight of the
layers above hardly changes. Thus, the temperature will change as
δT/T=δP/P−δρ/ρ = (r/D−4)δR/R, i.e., it
increases for D < r/4. (See KW, §33.2 for more detail.) This
instability leads to so-called thermal pulses on the asymptotic giant
branch (see below).
4 Contraction
For optically thin emission, like in molecular cloud (or neutrino
emission in a collapsing iron core), the material is roughly
isothermal (P ∝ ρ, i.e., Γ = 1 < [4/3]), and hence,
once unstable, collapse is inevitable.
Once the cloud becomes optically thick, further collapse is adiabatic
and hydrostatic equilibrium will eventually be attained (for molecular
hydrogen, Γ = [7/5], so still close to [4/3]).
Further instabilities set in when hydrogen is first dissociated and
then ionised.
As a star contracts on a thermal timescale (i.e., remaining in
hydrostatic equilibrium), ρ ∝ R−3 and T ∝ R−1,
and thus T ∝ ρ1/3. Hence, a star approaches degeneracy:
Pideal ∝ ρT, PNR ∝ ρ5/3, hence
lines of constant degeneracy have T ∝ ρ2/3. Denser
(lower-mass) stars will become degenerate earlier, and for brown
dwarfs, this happens before they become hot enough to ignite hydrogen
(see Fig. ).
For radiation-dominated stars, the contraction is along the same
direction, but they do not approach degeneracy: Prad ∝ T4, PER ∝ ρ4/3, hence lines of constant
degeneracy have T ∝ ρ1/3. Hence, the lack of turn-over in
Fig. 1 of lines starting at lower density
(more massive stars).
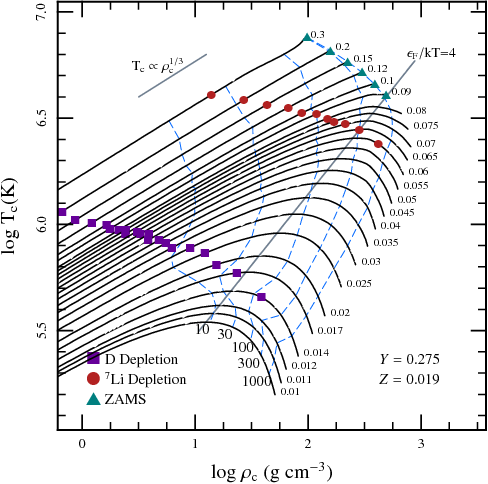
Figure 4.1: Trajectories of central conditions for low-mass
(M < 0.3 M
☉), fully convective stars as they approach the
main sequence or become brown dwarfs. Note how for fully
convective stars, whose internal structure in well described by a
n=1.5 (Γ = [5/3]) polytrope, the trajectories follow
the expected T ∝ ρ
1/3 track. Tracks turn over when
the conditions have become fairly degerate: Fermi energy E
F/kT ≅ 4. Taken from [], their Fig. 16
5 Low mass stars
After the main-sequence, the cores of low-mass stars become
degenerate, surrounded by a hydrogen-burning shell, and the envelopes
expand, making the stars red giants.
Shell burning
In a shell, the density and pressure drop very quickly, and hence
their properties depend mostly on the properties of the core.
Analogously to main-sequence stars, one can use homology arguments to
show how ρ, P, T, and L scale with Mcore and
Rcore. The easiest is the scaling for temperature, which,
assuming an ideal gas and using hydrostatic equilibrium,
|
T ∝ |
P
ρ
|
∝ |
1
ρ
|
|
GMcoreρH
Rcore2
|
∝ |
Mcore
Rcore
|
, |
| (5.1) |
where we used that the scalelength H can only scale with R core assuming homology. Since fusion is generally a steep
function of temperature, this means the luminosity will depend
sensitively on the core properties. As the envelopes of red giants
are mostly convective, and the photospheres have roughly fixed
effective temperature, the radius is also a strong function of core mass.
The other scalings depends on, e.g., the temperature-dependence of the
fusion process; if it is very steep, a small increase in, say, M core and thus T, will lead to a large increase in luminosity,
due to which the star will expand, lowering the density. For details,
see KW, §32.2.
Helium flash
The degenerate core will be heated by its surrounding shell, and be
nearly isothermal, with a slightly lower temperature in the centre due
to neutrino losses. When Mcore ≅ 0.45 M☉, the
temperature becomes hot enough for ignition, and runaway fusion
starts in a shell. As this region is only moderately degenerate,
convection kicks in relatively quickly, which limits the maximum
temperature reached and thus avoids a dynamic event (timescales for
entropy increase always remain larger than the dynamical timescale).
In the end, the star settles down as a core-helium burning giant, with
most of the luminosity still due to the hydrogen shell. We see such
sources as red-clump stars in metal-rich populations, and
horizontal-branch stars in metal-poor ones.
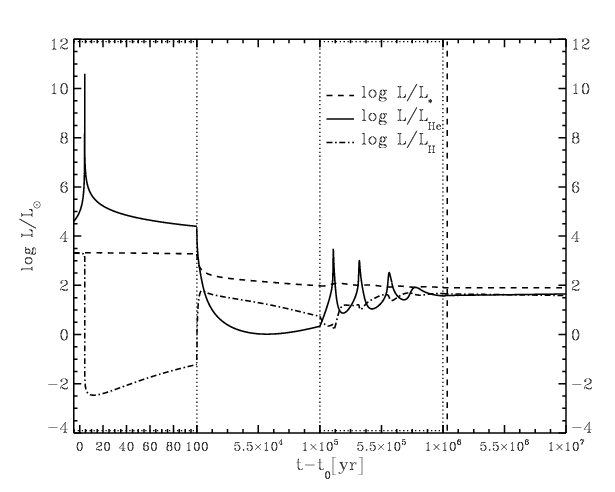
Figure 5.1: Luminosities during the helium flash. The initial spike
is due to the off-centre helium flash. Subsequent spikes occur
when inner layers are heated up sufficiently to ignite. As the
core is expanding, these reach less high temperatures and
luminosities. Note how the luminosity from the hydrogen shell
varies in the opposite sense of the helium luminosity, while the
luminosity emitted varies much more slowly. Taken from
[], their Fig. 2.
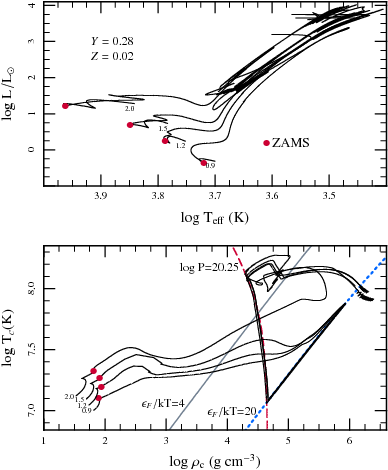
Figure 5.2: Evolution of low-mass stars. One sees the core density
and temperature converge for the different stars, increasing
during the red giant branch up to the helium flash. The flash
starts in an outer layer, at
ρ ≅ 4×10
5 g cm−3, i.e.,
logρ ≅ 5.6 ([]). This is close to where the
2 M
☉ track takes off and the density and temperature in
the shell should evolve similarly. The cores of the lower-mass
stars first expand at roughly constant degeneracy (i.e.,
essentially adjusting adiabatically to the decreasing weight of
the overlying layers), before the core is heated such that a
run-away occurs. From [], their
Fig. 14.
Double-shell burning
When two or more shells are present, they do not necessarily evolve at
the same rate, leading to changing separation (in mass coordinates),
and to thin shells that are geometrically unstable (see above).
This underlies the thermal pulses on the asymptotic giant branch.
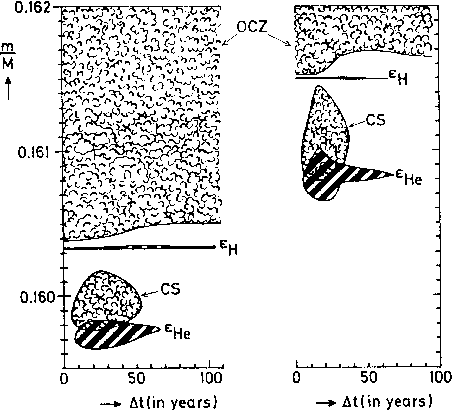
Figure 5.3: Evolution of the mass shells around the two shell sources
in a 5 M
☉ tar near the maximum of the first and sixth
thermal pulses. From KW, Fig. 33.4.
The Carbon flash (that doesn't happen)
Absent mass loss, for a sufficiently massive star, eventually the core
density and temperature would increase sufficiently to ignite carbon.
This happens as one approaches the Chandrasekhar mass, and in the
core, which has a lower ignition temperature due to its very high
density (note that the competition between neutrino cooling and
compressional heating also makes the temperature distribution less
uniform than was the case for a helium core). As one is at very high
degeneracy, the run-away destroys the whole core (and surrounding
envelope).
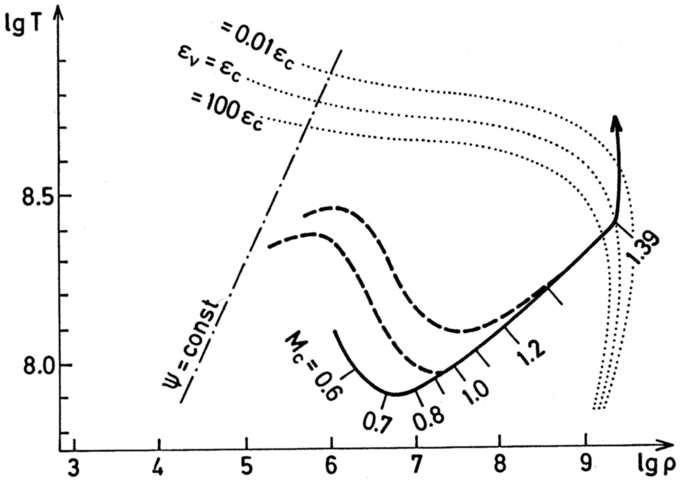
Figure 5.4: Temperature and density in the CO core of a 3 M
☉
star after central helium burning. The broken lines show
temperature stratifications at two instances. The core grows
until carbon is ignited. In real stars, mass loss prevents the
core from becoming this massive.
6 Ignition masses
A star with mass above the Chandrasekhar mass cannot be supported by
degeneracy pressure, hence such stars continue to contract, becoming
hotter, until fusion starts or some other process intervenes. Below
the Chandrasekhar mass, a star heats up until it ignites fusion or
becomes degenerate. The maximum temperature a star can have and still
become degenerate is T=1.3×109 K (A, §6.6).
The ignition mass is the minimum mass required to reach ignition. It
is ∼ 0.08 M☉ for hydrogen, ∼ 0.3 M☉ for
helium, ∼ 0.8 M☉ for carbon, and ∼ 1.36 M☉ for
neon []. All heavier fuels are only burnt by stars (or
cores of stars) above the Chandrasekhar mass.
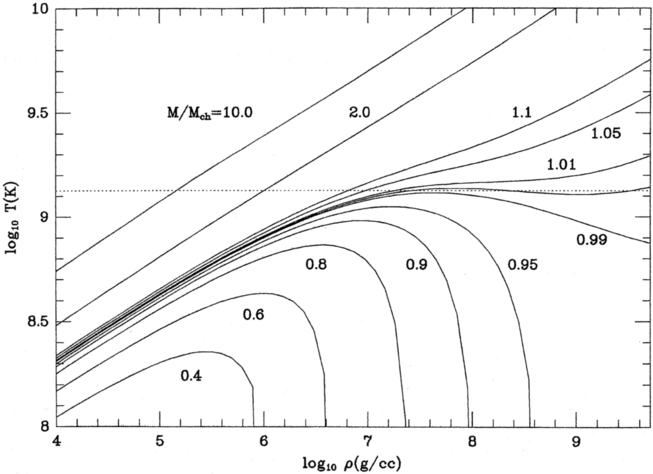
Figure 6.1: Effects of contraction on temperature and density. From
Arnett, his Fig. 6.3.
Burning stages
From Arnett, his table 6.2.
- Hydrogen burning (2×107 K,
(5…8)×1018 erg g−1): mostly helium (via p-p
or CNO; all CNO converted to N).
- Helium burning (1.5×108 K,
7×1017 erg g−1): mostly carbon and oxygen
(triple alpha, plus 12C(α,γ)16O,
with final abundance ratio strongly dependent on rate, and on extent
to which fresh helium is brought in at late stages (which would lead
to more oxygen).
- Carbon burning (8×108 K,
5×1017 erg g−1): mainly O, Ne, Mg, Si.
- Neon burning (1.5×109 K,
1.1×1017 erg g−1): mainly O, Mg. Starts with
photo-desintegration: 20Ne(γ,α)16 O, followed by 20Ne(α,γ)24Mg.
- Oxygen burning (2×109 K,
5×1017 erg g−1): mainly Si, S.
- Silicon burning (3.5×109 K,
(0…3)×1017 erg g−1): iron-peak
7 Intermediate mass stars
A M\ga2 M☉ forms a \ga0.3 M☉ helium core and thus
reaches ignition before becoming degenerate. Hence, these stars form
lower-luminosity red-clump stars than initially less massive stars
(for clusters with a slight spread in age, "double red clumps" have
been observed; see ). Their further evolution is
similar to that of lower-mass stars, though: they form CO cores and
become AGB stars, with the evolution terminated by fast mass loss in
the superwind. (The latter is still poorly understood theoretically;
.)
For M\ga8 M☉ (the mass is uncertain and depends on assumptions
about convection, overshoot, etc.), upon helium exhaustian, a
\ga0.8 M☉ carbon core is formed, which reaches carbon
ignition before becoming degenerate. Carbon fusion leaves a core
composed of mostly oxygen and neon. If this core becomes degenerate
before neon ignition (for core mass \la1.37 M☉), the star
becomes a "super AGB" star.
Electron-capture induced collapse
The further evolution of ONe cores depends on how much mass can be
accreted. If less than the Chandrasekhar mass, it will become a white
dwarf, while if it is more, it will reach such high densities that
electron captures start, which will lead to collapse. Note that like
for CO cores, neutrino cooling prevents the degenerate core from
becoming hot enough to ignite the next burning stage. Unlike for CO
cores, however, electron captures start to occur before the density
becomes high enough to ignite neon or oxygen burning. Oxygen burning
only starts as the core is already irreverably collapsing
[].
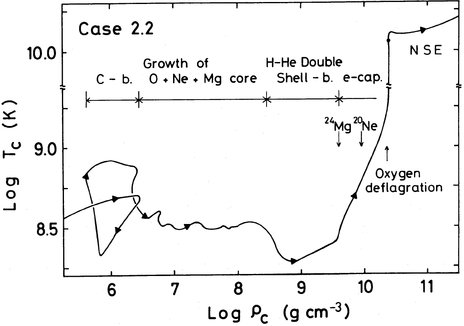
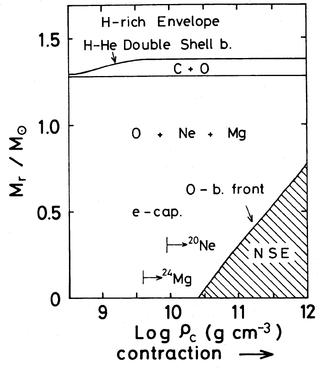
Figure 7.1: Evolution of central density and temperature of a ONe
core that is growing in size (left), and evolution during collapse
due to electron captures (right). From , his Figs 4
and 6.
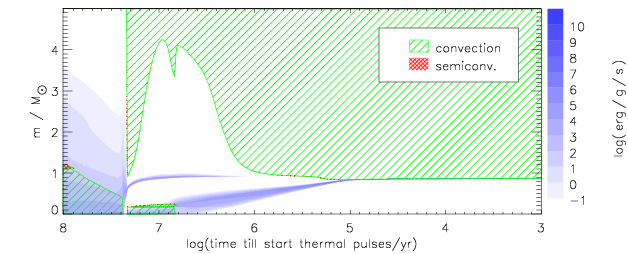


Figure 7.2: Time evolution for stars with masses of 5, 11.5, and
16 M
☉. Note the strong second dredge-up for the
11.5 M
☉ model, which greatly reduces the helium core mass,
and ensures that the star ends its life as a ONe white dwarf.
Taken from , their Fig. 1.
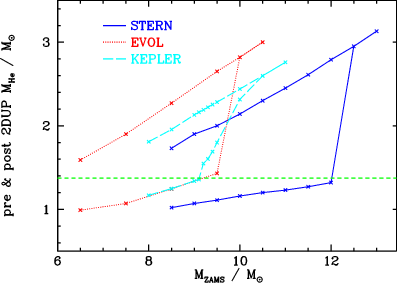
Figure 7.3: Helium core mass as a function of initial mass for
different stellar evolution codes, showing the effects of second
dredge-up. Taken from , their
Fig. 2.
8 Massive stars
Stars more massive than ∼ 8 M☉ ignite all phases of
nuclear burning non-degenerately, and end with iron core collapse,
leading either to a neutron star or a black hole. The details depend
not just on initial mass, but also on the amount of mass loss.
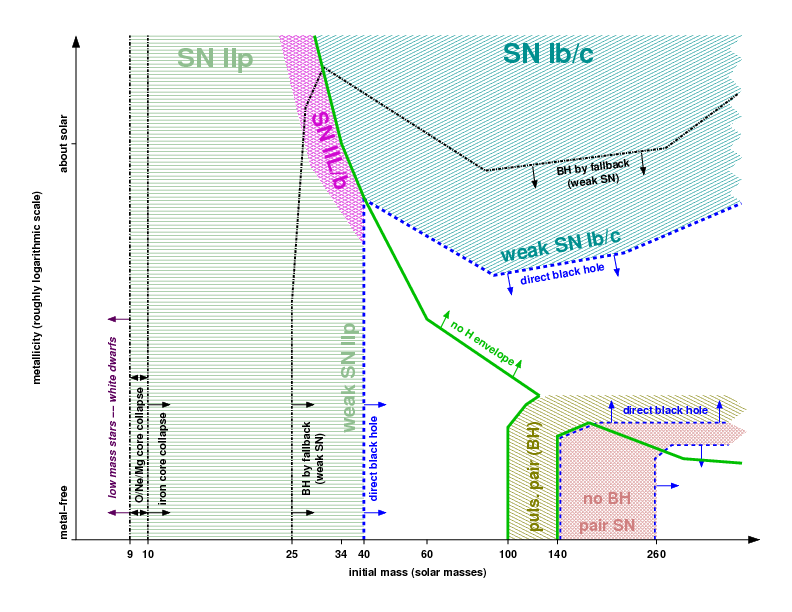
Figure 8.1: Final evolution as a function of mass and metallicity - the
latter influences the results mainly through the mass-loss rates.
From , their Fig. 2.
9 Very massive stars
Stars so massive that they produce oxygen cores of \ga40 M☉
(this may only be possible for very low-metallicity stars that
experienced little mass loss), pass through the pair-instability
region (see figure below and Fig. 1).
There, 〈γ〉 < [4/3], and the core becomes
unstable. It starts to collapse and reaches oxygen ignition. The
collapse may only be halted by the time the oxygen burning timescale
is less than the dynamic time, making the burning explosive. This
could lead to partial or total disruption of the star, or, if the
explosion is insufficiently energetic, to later disintegration and
(likely) direct collapse to a black hole.
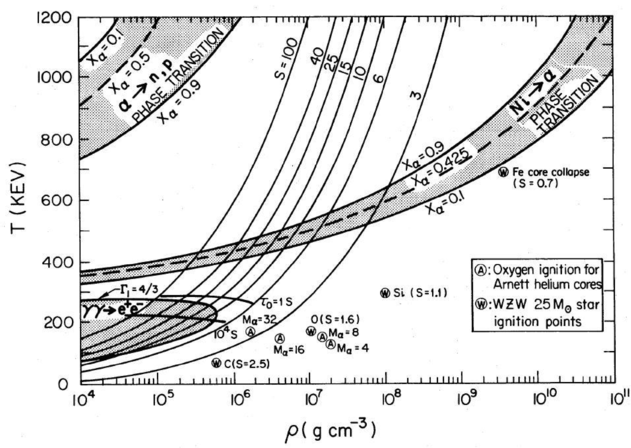
Figure 9.1: Isentropic lines for a oxygen/pair plasma, with regions
of interest indicated. From [], their
Fig. 3.
10 Binary evolution
Most stars increase in radius as they evolve, often drastically. If
in a binary, they may at some point overflow their Roche lobes,
leading to mass transfer to the companion. If this is stable, mass
transfer will be on the evolutionary timescale. If unstable, it can
be on the dynamical or thermal timescale. Masses transfer ceases when
the star stops trying to expand; in giants, this is when most of the
envelope has been transferred, and the remainder becomes so tenuous
that it shrinks. Thus, one generally is left with just the core of
the star. This process, and variations on it, is responsible for most
of the more interesting stars we observe.
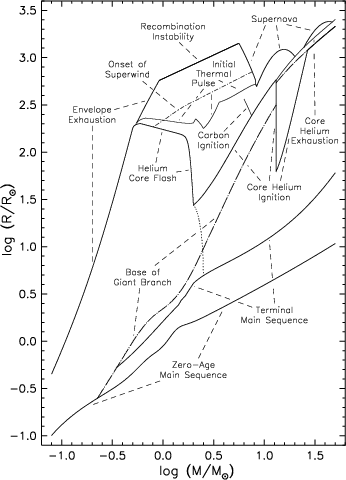
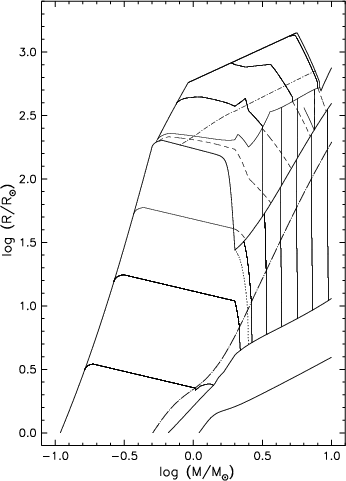
Figure 10.1: Radius evolution of stars of various masses. In the
left-hand panel, the one unmarked dotted line between ‘helium core
flash’ and ‘core helium ignition’ marks the division between those
helium cores (at lower masses) which evolve to degeneracy if
stripped of their envelope, and those (at higher masses) which
ignite helium non-degenerately and become helium stars. In the
right-hand panel, core masses interior to the hydrogen-burning shell
are indicated with solid lines, and dashed lines those interior to
the helium-burning shell. Solid lines intersecting the base of the
giant branch (dash-dotted curve) correspond to helium core masses of
to 0.15, 0.25, 0.35, 0.5, 0.7, 1.0, 1.4, and 2.0 M
☉; those
between helium ignition and the initial thermal pulse to 0.7, 1.0,
1.4, and 2.0 M
☉, and those beyond the initial thermal pulse
to 0.7, 1.0, and 1.4 M
☉. Dashed lines between helium
ignition and initial thermal pulse correspond to carbon-oxygen core
masses of 0.35, 0.5, 0.7, 1.0, and 1.4 M
☉. Beyond the
initial thermal pulse, helium and carbon-oxygen core masses
converge, with the second dredge-up phase reducing helium core
masses above ∼ 0.8 M
☉ to the carbon-oxygen core. From
, his Figs 1 and 2.
Mass loss and tranfer
Consider a star that looses or transfers mass at some rate · M.
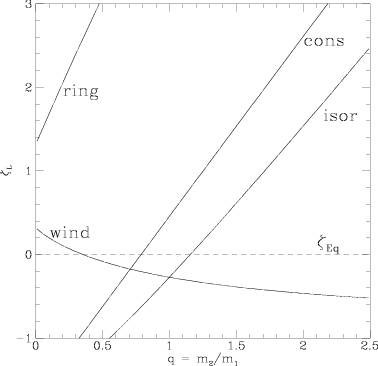
Figure 10.2: ζ
L ≡ ∂lnR
L/∂lnM
2 as a
function of mass ratio, with all mass transfer through a single
channel: conservative (cons); isotropic wind from donor star
(wind); isotropic re-emission of matter, from vicinity of
`accreting' star (iso-r). (Also shown is a ring formation,
indicative of mass loss from an outer Lagrange point). From
, their Fig. 4.
Effect on orbit
The angular momentum of an orbit is given by
J=(M1M2/M)√{GMa}, and thus,
|
|
J
|
= |
M1
|
+ |
M2
|
− |
1
2
|
|
M
|
+ |
1
2
|
|
a
|
|
| (10.1) |
Conservative mass transfer: · M1=−· M2, · M=0, · J=0. Thus,
|
|
a
|
= 2 |
M2−M1
M1M2
|
|
⋅
M
|
2
|
= 2(q−1) |
M2
|
, |
| (10.2) |
where q=M2/M1 is the mass ratio between the donor (star 2) and the
accretor (star 1). For donors less massive than the accretor, the
orbit expands upon mass transfer (remember that · M2 < 0).
Looking at the Roche lobe for a less massive donor, for which
RL ≅ 0.46a(M2/M)1/3 [], one finds
|
|
RL
|
= |
a
|
+ |
1
3
|
|
M2
|
= 2 | ⎛
⎝
|
q− |
5
6
| ⎞
⎠
|
|
M2
|
, |
| (10.3) |
showing that the Roche lobe, as expected, grows a little slower than
the orbital separation. (An analysis valid for all q would use the
approximation of [], RL/a ≅ 0.46q2/3/[0.6q2/3+ln(1+q1/3)].)
Spherically symmetric wind: · M2=· M, · M1=0, · J=(· M2/M2)(M1/M)J. Hence,
|
|
a
|
= 2 | ⎛
⎜
⎝
|
M2M
|
− |
M2
|
+ |
2M
| ⎞
⎟
⎠
|
=− |
M
|
. |
| (10.4) |
Thus, for mass loss (· M < 0), the orbit expands.
Spherically re-emitted wind: · M2=· M, · M1=0, · J=(· M2/M1)(M2/M)J (idea is that accretor cannot
handle mass transferred to it and re-emits it as a wind). Hence,
|
|
a
|
= 2 | ⎛
⎜
⎝
|
M1M
|
− |
M2
|
+ |
2M
| ⎞
⎟
⎠
|
= |
2q2−2−q
1+q
|
|
M
|
. |
| (10.5) |
Hence, orbit expands for q < (1+√{17})/4=1.28 (with again a
somewhat lower value for increasing Roche-lobe radius), i.e., it is
less quickly unstable than for conservative mass transfer. For a more
detailed analysis, see .
Effect on stellar radius
If the mass is lost from the outside of a star, the star becomes
initially smaller, but on a hydrodynamic timescale it will partially
re-expand in responds to the decreased pressure. Which effect
dominates depends on the internal structure of the star. Generally,
for thermal envelopes, the stars shrinks inside its Roche lobe,
re-expanding only on the thermal timescale, typically to nearly its
original size (especially for giants). For more detail, see
. However, a complication for thermal-timescale mass
transfer is that, if the secondary is substantially less massive, it
cannot accrete sufficiently fast and will bloat itself. For massive
stars, for M2/M1\la0.7, this leads to contact, and almost
certainly further mass loss and/or a merger
[,,].
Completely convective stars, or stars with deep convective layers,
however, increase in size upon mass loss. For completely convective
stars, which are described well by polytropes with P=Kργ
with γ = [5/3] (and thus n=1.5), this follows immediately
from the mass radius relation: R ∝ M−1/3 (true for constant
K, i.e., for constant entropy or completely degenerate,
non-relativistic gas). Comparing this to the change in Roche lobe for
conservative mass transfer, one sees that stability requires that
|
2 | ⎛
⎝
|
q− |
5
6
| ⎞
⎠
|
< − |
1
3
|
⇔ q < |
2
3
|
for n=1.5. |
| (10.6) |
From the work of [], it is indeed clear that for low-mass
white dwarfs, dynamical instability sets in for q > [2/3]. For
higher mass accretors (M1 >~0.3 M☉), the mass-transfer
rate rapidly becomes super-Eddington, meaning some mass has to leave
the system. As shown above, this implies the binary expands more and
it is easier to keep mass transfer stable. [] find
that, roughly, stability requires q <~0.7−0.1(M1/M☉).
Common-envelope evolution
When dynamically unstable mass transfer starts, the stars enter a
common envelope. This will lead to a merger unless one envelope is
relatively loosely bound, e.g., if the donor is a red giant. The
process is still very uncertain, and usually an energy criterion is
used to decide whether or not a complete merger occurs. We write the
initial orbital energy as Eorb,i=GM1M2/2ai, the
final one as Eorb,f=GM1,cM2/af, and the
envelope binding energy as Ee=GM1M1,e/λR1,e. Taking M1,e=M1−M1,c, a roche-lobe filling
star (R1,e=RL), and assuming an efficiency α CE=Ee/(Eorb,f−Eorb,i), one finds a total
shrinkage of the orbit,
|
|
af
ai
|
= |
M1,c
M1
|
| ⎡
⎣
|
1+ |
2
αCEλ
|
|
ai
RL
|
|
M1−M1,c
M2
| ⎤
⎦
|
−1
|
|
| (10.7) |
This shrinkage is usually very large. Tracing back the evolution of
double helium white dwarfs, , found that it cannot hold
for the first mass-transfer phase. They proposed an alternative
description based on angular momentum loss, but this was criticised
strongly by []. Overall, though, the conclusion stands
that for not too extreme mass ratios, mass transfer is stabilised
somehow (perhaps by irradiation driven winds; ).
Angular momentum loss
Two stars can be driven closer by angular-momentum loss. For
gravitational radiation (in a circular orbit),
|
− |
J
|
= |
32 G3
5c5
|
|
M1M2(M1+M2)
a4
|
, |
| (10.8) |
implying a merger time of
1.05×107 yr(M/M☉)−2/3(μ/M☉)−1(P/1 hr)8/3,
where μ = M1M2/(M1+M2) is the reduced mass, and P the orbital
period. Thus, to merge within a Hubble time requires
P\la0.5 d.
For binaries with low-mass stars, angular momentum can also be lost
by "magnetic braking" - a solar-like wind coupled to a magnetic
field. This mechanism is usually described by semi-empirical
relations, which are calibrated using the rotational evolution of
single stars and using population synthesis models for binaries.
Supernova explosions
One can solve the effect of a spherically symmetric supernova
explosion by consiering that, for instantaneous mass loss, the
velocities of the two stars remain the same, but their mutual
attraction has decreased. Thus, the instantaneous position will
become the periastron of the new orbit. For given mass loss ∆M,
| |
|
| | (10.9) |
| |
|
|
G(M1+M2−∆M)
af
|
|
1+e
1−e
|
= |
G(M1+M2)
ai
|
. |
| | (10.10) |
|
Solving this yields
i.e., the orbit is unbound if ∆M > [1/2](M1+M2) (as can be
seen more easily from the Virial Theorem). The binary also gets a
recoil kick, of
|
∆γ = |
M2v2−(M1−∆M)v1
M1+M2−∆M
|
=ev1. |
| (10.12) |
Unfortunately, the assumption that supernova explosions are
spherically symmetric seems rather poor, since single radio pulsars
have large space velocities, of several 100 km s−1. As a
result, binaries likely unbind even when relatively little mass is
lost, and, conversely, may remain bound even if a large amount of mass
is lost (indeed, the latter may be a requirement to understand
low-mass X-ray binaries, in which neutron stars accrete from low-mass
companions). There is fairly strong evidence, however, that some
supernovae do not impart (large) kicks, possibly those due to electron
capture (, and references therein).
Tidal stability
For close binaries, tides will circularise the orbit. This is not
possible if the mass ratio is too small. Stability requires that some
angular momentum transfer from the orbit to the star changes the
stellar rotation faster than the orbital one. Since J orb=(M1M2/M)√{GMa} ∝ Ω−1/3 and J star=IstarΩ ∝ Ω, stability requires that
Jorb > 3Jstar. For low-mass stars, binaries with mass
ratio q <~0.09 are unstable [].
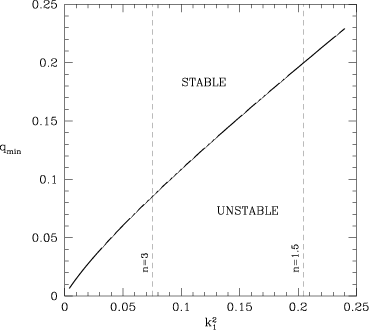
Figure 10.3: Minimum mass ratio required for tidal stability as a function
of gyration radius. From , his
Fig. 1.
Rapid rotation
Tidal synchronisation leads to rapid rotation. For low-mass stars,
this leads to increased activity, some increase in size, and a larger
stellar wind (and thus angular momentum loss; magnetic breaking).
For massive stars, rotation induces mixing []. For
fairly massive stars, just brings up nitrogen. For M\ga50 M☉
in a P\la2 d binary, centrally produced helium is efficiently
mixed. As a result, these stars may burn completely to helium, and a
lower-mass companion might evolve faster!
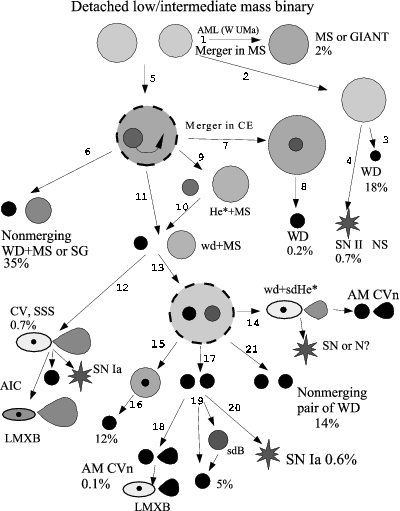

Figure 10.4: Possible outcomes for low and
intermediate-mass binaries. , Fig. 2 and 3.
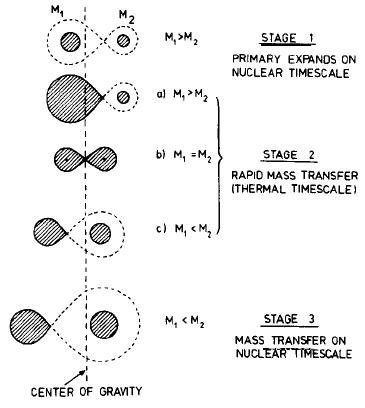
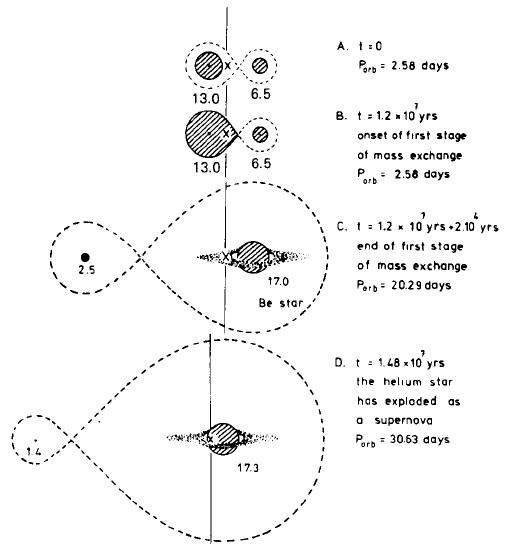
Figure 10.5: Conservative evolution of a massive binary (left) and
formation of a Be X-ray binary (right). From , their
Figs. 24 and 25.
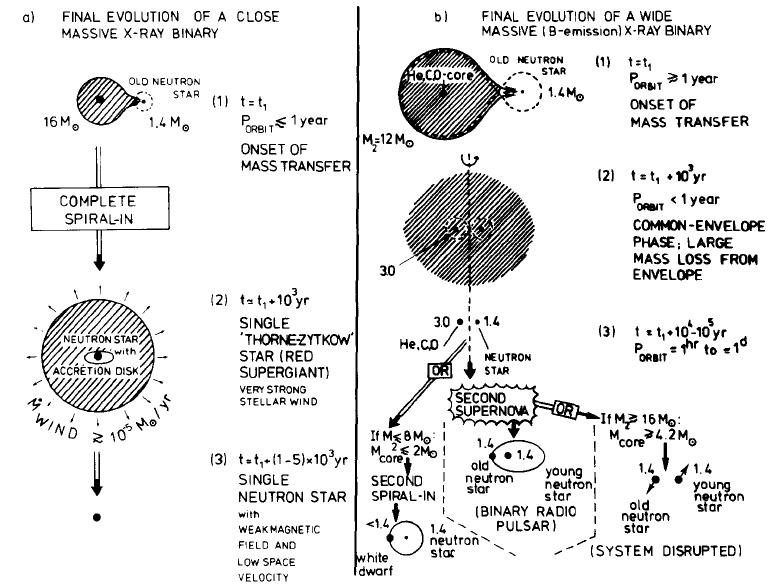
Figure 10.6: Further evolution of X-ray binaries with short (left) and
long (right) orbital periods. From Bhattacharya & Van den Heuvel (), their
Figs. 32.
11 Arnett's semi-analytical supernova lightcurves
We follow A96 and consider a ball of gas with initial radius R0
that is homologously expanding at constant velocity vsc, and
has an initial thermal energy E0. The first law of
thermodynamics can be written as,
where E is the total energy, V ≡ [(4π)/3]R3 is the
volume, P the pressure, ϵ the energy generation rate (by
radioactive decay) per unit mass, M the ejecta mass, and L the
luminosity.
Assume the energy and pressure are dominated by
radiation, i.e., E ≅ E, and P ≅ [1/3]E.
Dividing by E on both sides and using homology, one finds,
|
4 |
T
|
+3 |
R
|
+ |
1
3
|
3 |
R
|
= 4 | ⎛
⎜
⎝
|
T
|
+ |
R
| ⎞
⎟
⎠
|
= |
1
τh
|
− |
1
τd
|
, |
| (11.2) |
where the heating timescale τh=E/ϵM and the
luminosity due to cooling timescale due to diffusion of photons is
τd=E/Ldiff. The latter is also given by,
|
τd = |
κM
βc R
|
= τd,0 |
R0
R
|
, |
| (11.3) |
where in the second equality one implicitly assumes constant opacity.
For a constant density ball, β = 13.8.
The above suggests to consider the evolution of the product (TR)4.
We assume its spatial (x ≡ r/R) and time dependence can be split,
|
R4(t) T4(x,t) = R04 T04 ϕ(t) Ψ(x). |
| (11.4) |
For constant density ρ = M/[4/3]πR3 and constant opacity κ,
In terms of these functions, the thermal energy can be written as,
|
E = | ⌠
⌡
|
R
0
|
aT(r,t)44πr2 dr = 4πR3 aT(0,t)4 | ⌠
⌡
|
1
0
|
Ψ(x)x2 dx = |
4
π
|
R03 aT04 |
R0
R
|
ϕ(t) = E0 |
R0
R
|
ϕ(t) |
| (11.6) |
where we used that ∫01Ψ(x)x2 dx=1/π2. The factor
R0/R accounts for adiabatic expansion and ϕ(t) for radiation
loss and radioactive heating. Given this, the luminosity is given by
Supposing the initial thermal energy is of order the kinetic energy,
i.e., E0 ≅ [1/2]Mvsc2, the initial
lumonosity L0=E0/τd,0 ∝ vsc2R/κ
is independent of mass, but proportional to radius. Faster ejections
(larger energy) from larger stars (faster diffusion) give more
luminous transients.
Diffusion and heating
With just diffusion and heating, one has
|
|
(TR)4
|
= |
ϕ
|
= |
1
τh
|
− |
1
τd
|
⇔ |
ϕ
|
= | ⎡
⎣
|
ϵ/ϵ0
τh,0ϕ
|
− |
1
τd,0
| ⎤
⎦
|
|
R
R0
|
, |
| (11.8) |
where we tried to write in terms of ratios on the right-hand side,
with ϵ/ϵ0 capturing the time dependence of the
heating process (and where we again implicitly assumed constant
opacity).
Ignoring heating, an analytic solution is possible. Using
that τd=τd,0(R0/R)=τd/(1+vsct/R0), and
defining an expansion timescale τe=R/vsc, one finds
|
ϕ = exp | ⎛
⎝
|
− |
t
τd,0
|
− |
t2
2τeτd,0
| ⎞
⎠
|
. |
| (11.9) |
Generally, τd,0 >> τe, and thus for
t > τe, the lightcurve is essentially a Gaussian, with a
timescale that is the geometric mean of the expansion and diffusion
times scales, τexp=√{τhτ d,0} ∝ √{κM/vsc}. Slower, more massive
ejections lead to longer transients.
Including heating, the integration needs to be done numerically.
However, generally, one expects maximum to occur when · ϕ=0,
i.e., when 1/τh=1/τd (of course, if heating is
too small, this maximum after explosion never happens). From their
definitions, the timescales match when L=ϵM. Thus, maximum
luminosity gives a measure of the total amount of radioactive decay -
"Arnett's rule." (This will be an underestimate if the opacity is
decreasing with time - or if this is happening effectively due to
recombination.)
Including recombination
At some temperature Ti, material will recombine and become
essentially transparent. If this happens inside the cloud, then this
will effectively be at optical depth zero, and the photosphere would
be at Teff4 ≅ 2Ti4. As more matter recombines, the
photosphere will move in, with recombination and advection ("freed"
radiation) giving additional sources of luminosity. At this time, one
will have,
|
Ldiff+Ladv+Lrec = Lmin = 4πRi2σ2Ti4, |
| (11.10) |
where Ri=xiR is the radius of the recombination front, and where
we used the subscript "min" as a reminder that the luminosity cannot
be lower than this value for this radius.
The luminosity due to recombination is
|
Lrec = −4πRi2 |
⋅
R
|
i
|
ρQ = −3xi2 |
⋅
x
|
i
|
|
4π
3
|
R3ρQ = −3xi2 |
⋅
x
|
i
|
MQ, |
| (11.11) |
where Q is the energy release per unit mass due to recombination.
For the advection and diffusion terms, the results depend on whether
the front moves slow or fast compared to the time to adjust the
overall temperature structure. Generally, though, L diff = E/τd and,
but the total thermal energy E and diffusion timescale
τd may now depend on xi. In consequence, not only the
differential equation for ϕ has to be solved, but also one for
the recombination front position xi. The latter can be derived
from the constraint that the additional luminosity
Lrec+Ladv has to match the excess luminosity L min−Ldiff, or
|
− |
⋅
x
|
i
|
| ⎡
⎣
|
3xi2MQ+ |
∂E
∂xi
| ⎤
⎦
|
= 4πR2 xi2 2σTi4 − |
E
τd
|
. |
| (11.13) |
Below, we will also use the timescale on which the initial energy
would be radiated at an effective temperature of 21/4Ti,
|
τi,0 ≡ |
E0
Lmin,0
|
= |
|
= |
4R0
π2 c
|
|
T04
2Ti4
|
. |
| (11.14) |
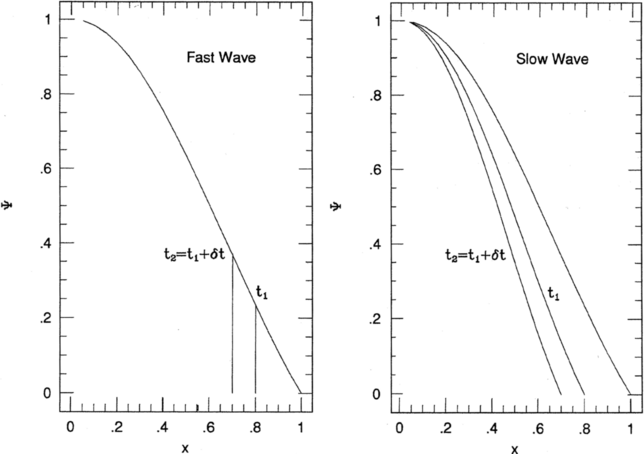
Figure 11.1: Fast and slow approximation to a recombination wave. From
A96, his Fig. 13.7.
Slow recombination front
If the recombination front moves slowly, photon diffusion inside it
will ensure the temperature structure adjusts to
its new outer boundary, Ri=xiR, with the same spatial structure
([T(x)/T(0)]4=Ψ(x)). Thus, the total thermal energy will
be
|
E = 4πR3 aT(0,t)4 | ⌠
⌡
|
xi
0
|
Ψ(x/xi)x2 dx = E0 |
R0
R
|
ϕ(t)xi3, |
| (11.15) |
where ϕ(t) accounts for changes in central properties due to the
recombination wave and associated energy loss. Given this, the
advection luminosity is given by,
|
Ladv = − |
⋅
x
|
i
|
|
∂E
∂xi
|
= −3xi2 |
⋅
x
|
i
|
E0 |
R0
R
|
ϕ(t). |
| (11.16) |
Since the size is decreasing, the luminosity due to photon diffusion
also changes, becoming
|
Ldiff = |
E
τd
|
= |
E0
τd,0
|
ϕ(t)xi, |
| (11.17) |
where we used that τd=τd,0(R0/R)xi2, with the
dependence on xi2 reflecting the dependence of τd on M/R (for constant
density the mass enclosed within the recombination front scales with
xi3). The differential equations to be solved thus become,
| |
|
|
|
ϵM
E0ϕxi3
|
|
R
R0
|
− |
1
τd,0xi2
|
|
R
R0
|
, |
| | (11.18) |
| |
−3xi2 |
⋅
x
|
i
|
| ⎡
⎣
|
MQ+E0 |
R0
R
|
ϕ | ⎤
⎦
|
|
|
|
| 4πR2 xi2 2σTi4 − |
E0
τd,0
|
ϕxi. |
| | (11.19) |
|
Simplifying,
| |
|
|
| ⎡
⎣
|
ϵ/ϵ0
τh,0ϕxi3
|
− |
1
τd,0xi2
| ⎤
⎦
|
|
R
R0
|
|
| | (11.20) |
| |
|
|
|
|
xi2
τi,0
|
| ⎛
⎝
|
R
R0
| ⎞
⎠
|
2
|
− |
ϕxi
τd,0
|
|
|
| | (11.21) |
|
Fast recombination front
For a fast-moving recombination front, the temperature structure
inside will not react to the fact that the outer parts are being
chopped off. The total thermal energy inside the recombination
wave is,
|
Ex < xi = 4πR3 aT(0,t)4 | ⌠
⌡
|
xi
0
|
Ψ(x)x2 dx = E0 |
R0
R
|
ϕ(t) π2 | ⌠
⌡
|
xi
0
|
Ψ(x)x2 dx, |
| (11.22) |
and thus the advection luminosity is given by,
|
Ladv = − |
⋅
x
|
i
|
|
∂Ex < xi
∂xi
|
= −3xi2 |
⋅
x
|
i
|
|
π2
3
|
Ψ(xi) E0 |
R0
R
|
ϕ(t). |
| (11.23) |
The luminosity due to photon diffusion from the inside now changes
only because we are evaluating it at a different position, becoming
|
Ldiff = L0diff |
|−x2∂Ψ/∂x|xi
|−x2∂Ψ/∂x|1
|
= |
E0
τd,0
|
ϕ(t) | ⎢
⎢
|
−x2 |
∂Ψ
∂x
| ⎢
⎢
|
xi
|
= |
E0
τd,0
|
ϕ(t)π2I(xi). |
| (11.24) |
where L0diff is the diffusion luminosity we would obtain
ignoring the recombination wave, and where we have used that
[−x2∂Ψ/∂x]xi = (1/π)sin(πxi)−xicos(πxi) = π2I(xi)
(where π2I(xi)=π2∫0xiΨ(x)x2dx is the normalised
integral).
The differential equations to be solved now become,
| |
|
|
|
ϵM
E0ϕπ2I(xi)
|
|
R
R0
|
− |
1
τd,0
|
|
R
R0
|
, |
| | (11.25) |
| |
−3xi2 |
⋅
x
|
i
|
| ⎡
⎣
|
MQ+E0 |
R0
R
|
ϕ |
π2
3
|
Ψ(xi) | ⎤
⎦
|
|
|
|
| 4πR2 xi2 2σTi4 − |
E0
τd,0
|
ϕπ2I(xi). |
| | (11.26) |
|
Simplifying,
| |
|
|
| ⎡
⎣
|
ϵ/ϵ0
τh,0π2I(xi)
|
− |
1
τd,0
| ⎤
⎦
|
|
R
R0
|
|
| | (11.27) |
| |
|
|
|
|
xi2
τi,0
|
| ⎛
⎝
|
R
R0
| ⎞
⎠
|
2
|
− |
ϕπ2I(xi)
τd,0
|
|
|
MQ
E0
|
+ |
R0
R
|
ϕ |
π2
3
|
Ψ(xi) |
|
|
| | (11.28) |
|
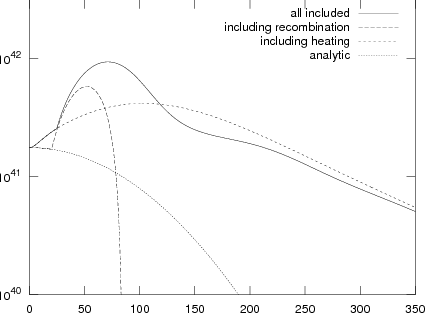
Figure 11.2: Comparison of explosions with and without recombination and
heating by radioactive decay. Note that I could not reproduce all
curves in A96 in detail, in particular not for the "slow" case.
Still, the general trends are clear and should be correct.
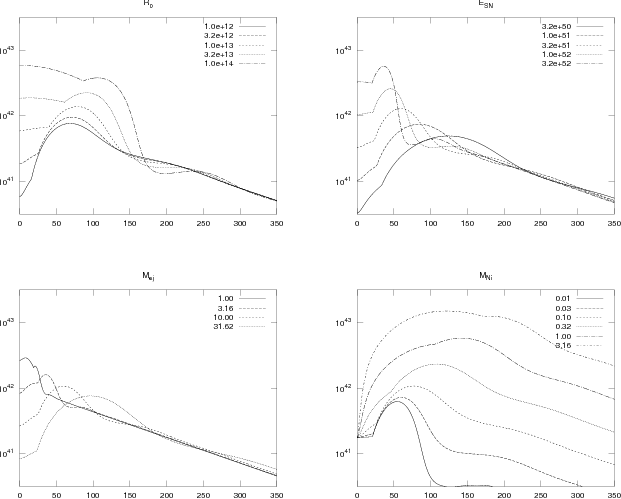
Figure 11.3: Semi-analytic lightcurves for supernovae with varying
properties. Those not varied are held fixed at those inferred for
SN 1987A by A96 (his Table 13.2): M
ej=15 M
☉, E
SN=1.7×10
51 erg, R
0=3×10
12 cm,
κ = 0.2
cm2 g1, M
Ni=0.075 M
☉,
T
ion=4500
K, Q
ion=13.6
eV nucleon−1. Ignored is losses of gamma
rays, and hence the luminosity at late times is
overestimated.
File translated from
TEX
by
TTH,
version 4.03.
On 27 Mar 2013, 12:46.